Teoria del contatto

 

back to homepage

 

 

Date due curve

 

C : x(t) = (f₁(t), f₂(t),f₃(t))

C* : x(t*) = (g₁(t*), g₂(t*),g₃(t*))

 

che hanno un punto P in comune che corrisponde rispettivamente a t₀ e t₀* ci sono due possibilità:

 

a)      Le tangenti a C e C* sono differenti

b)      Le tangenti a C e C* coincidono

 

In entrambi i casi si ha:

 

x(t₀) = x(t₀*)

 

Nel solo caso b) si ha che i due vettori 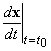 e 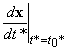sono paralleli.

Considerando come parametro la lunghezza d’arco s scriviamo:

 

[0704221915]            C : x(s) = (α₁(s), α₂(s), α₃(s))

[0704221915]            C* : x(s*) = (β₁(s*), β₂(s*), β₃(s*))

 

Queste rappresentazioni parametriche sono di classe r, indipendentemente dal parametro utilizzato.

Denotiamo con s₀ e s₀* il valore del parametro per P₀

In virtù del particolare parametro usato abbiamo:

 

α_i(s₀) = β_i(s₀*)

 

 

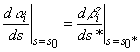
Si ha contatto di ordine m (esattamente) tra due curve C, C* nel punto P₀ se, usando la rappresentazione 0704221915 si ha, in P₀:

 

α_i(s) = β_i(s*)

 

 

e se esiste anche la derivata di ordine m+1 e si ha:

 

 

Un contatto del primo ordine è detto anche un contatto ordinario; un contatto di secondo ordine è anche detto contatto stazionario o osculazione; un contatto di terzo ordine è anche detto osculazione stazionaria o superosculazione.

Il contatto di ordine m-esimo non è altro che la coincidenza delle approssimazioni di Taylor di grado m-esimo alle due curve.

Definiamo ora superficie un insieme di punti in uno spazio euclideo che in un intorno di ogni punto può essere rappresentata nella forma:

 

G(x₁,x₂,x₃) = 0

 

dove G è una funzione di classe m ≥ 1 le cui derivate parziali del primo ordine non si annullano identicamente in alcun punto.

Si ha contatto di ordine m (esattamente) tra una curva e una superficie nel punto P₀ se esiste almeno una curva C* sulla superficie S che ha un contatto di ordine m con la curva data C nel punto P₀ e non esiste una curva su S con contatto di ordine maggiore di m con C.

Un piano che ha contatto di primo ordine con una curva C in P₀ deve passare per la tangente a C in P₀. In ogni punto di C esiste un intero fascio di piani di tale tipo, che include il piano osculatore.

Una curva ha contatto di secondo ordine (almeno) in ogni suo punto col sul piano osculatore.

Sia C : x(s) = (α₁(s), α₂(s), α₃(s)) la rappresentazione parametrica di classe r ≥ m con lunghezza d’arco s come parametro, che ha in comune un punto P₀ : s = s₀ con una superficie S che, in un intorno di P₀ ha una rappresentazione G(x₁,x₂,x₃) = 0 di classe r ≥ m. Allora C ha contatto di ordine m (esattamente) con S in P₀ sse la funzione

 

p(s) = G(α₁(s), α₂(s), α₃(s))

 

e le sue derivate rispetto a s, fino alla m-esima inclusa, si annullano in P₀ mentre la derivata (m+1)-esima, se esiste, non si annulla.

Sia C una curva di classe r ≥ m + 1 che ha contatto di ordine m con una superficie S di classe r in un punto P₀. Se m è pari allora C percia S in P₀. Se m è dispari allora, in un intorno di P₀ C giace da un lato di S.

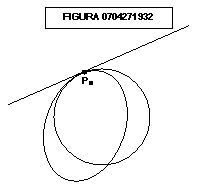
E’ perfettamente possibile che due curve che hanno la stessa tangente o una curva e una superficie si attraversino; si osservi la figura 0704271932:

 

 

Si osservi la figura 0704232005:

 

 

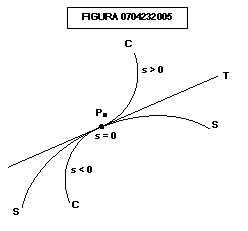
In essa le curve C ed S (quest’ultima può anche essere vista come la sezione di superficie) hanno in comune la tangente T, e C percia S. Posto il valore del parametro s eguale a zero in corrispondenza di P₀, nella parte inferiore a S avremo valori negativi di s mentre nella parte superiore avremo valori positivi.

In conseguenza della formula di Taylor abbiamo:

 

[0704232021]           

 

perché, in conseguenza del teorema [0704232020], in caso di contatto di ordine m tutte le derivate di p(s) di ordine fino ad m si annullano identicamente in P₀ mentre la derivata (m+1)-esima non si annulla. Per la continuità della (m+1)-esima derivata, in un intorno di P₀ sufficientemente piccolo (per |s| sufficientemente piccolo) la (m+1)-esima derivata è parimenti diversa da zero e, poiché non attraversa lo zero, avrà lo stesso segno poco prima e poco dopo P₀.

Dato θ compreso tra 0 ed 1 e |s| < ε si ha che  comprende derivate dello stesso segno per valori di s poco prima e poco dopo P₀.

Supponiamo che m sia pari. Allora m+1 è dispari e s^m+1 sarà minore di zero per valori di s inferiori a zero (tratto di curva precedente P₀) mentre sarà maggiore di zero per valori di s maggiori di zero (tratto di curva successivo a P₀). Per cui p(s) avrà segno differente prima e dopo P₀. Per definizione p(s) ha valore zero in P₀, e quindi la diversità di segno vuol dire che esistono punti di C sopra e sotto S.

Se invece m è dispari allora m + 1 è pari e il segno di p(s) è lo stesso poco prima e poco dopo P₀, ciò che implica che C giaccia da un unico lato di S.

Consideriamo una curva C : x(s) dove s è la lunghezza d’arco. Sia P un punto comune con una sfera S di raggio R con centro M. Denotato con a il vettore posizione di M possiamo rappresentare S nella forma:

 

[0704221949]            G(x₁,x₂,x₃) = (x – a) ⋅ (x – a) – R² = 0

 

Perché si abbia contatto del primo ordine tra C ed S in P deve essere in P:

 

[0704221950]           

 

cioè il centro M di ogni sfera che abbia contatto del primo ordine con C giace nel piano normale alla curva in P. Il vettore a è ora:

 

[0704222003]            a = x + αp + βb

 

Assumiamo ora che la curvatura κ in P sia diversa da zero. Perché si abbia contatto del secondo ordine tra C e la sfera S in P, in aggiunta alla 0704221950 deve essere:

 

[0704221951]           

 

Introducento la 0704221950 nella 0704221951 troviamo la condizione:

 

1 – ακ = 0

 

e cioè:

 

α = ρ

 

Questo significa che la famiglia di sfere con doppio parametro α,β con centri dati dalla 0704222003 che hanno contatto almeno del primo ordine con C a P contiene una famiglia di sfere con unico parametro  che ha contatto di secondo ordine almeno con C in P; il vettore posizione dei centri di questa famiglia di sfere è:

 

[0704222005]            a = x + ρp + βb

 

dove il parametro è dato da β. La rappresentazione della 0704222005 è una linea parallela alla binormale e passante per il centro di curvatura corrispondente a P, chiamata asse polare di una curva in un punto.

Perché C abbia contatto di terzo ordine con una sfera S in P, in aggiunta a 0704221959 e a 0704221951 deve essere:

 

[0704221952]           

 

Inserendo la 0704222005 nella 0704221952 otteniamo:

 

ρκ̇ + βκτ = 0

 

e dunque, se τ ≠ 0 in P,

 

[0704221953]           

 

Questo significa che la famiglia monoparametrica di sfere con centri 0704222005 che ha contatto del secondo ordine con C in P, in generale contiene solo una sfera S₀ che ha contatto del terzo ordine (almeno) con C n P. S₀ è chiamata sfera osculatrice di una curva in un punto.

Inserendo il valore di β ottenuto in 0704221953 troviamo il vettore posizione a del centro di S₀:

 

[0704222006]            a = x + ρp + b

 

Se κ̇ = 0 in P il centro di S₀ giace nel piano osculatore di C in P e coincide con il centro di curvatura.

Dalla 0704222006 otteniamo il raggio R_S di S₀:

 

[0704222007]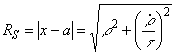           

 

Se la curvatura di una curva è costante il raggio della sfera osculatrice è costante. L’elica circolare è di questo tipo.

Possiamo sintetizzare i risultati precedenti come segue:

Il centro di una qualsiasi sfera che ha contatto di primo ordine (almeno) con una curva C in un punto P giace nel piano normale. Il centro di una qualsiasi sfera che ha contatto di secondo ordine (almeno), con κ > 0, giace sull’asse polare della curva; tutte queste sfere intersecano il piano osculatore lungo il circolo di curvatura di C che ha contatto di secondo ordine (almeno) con la curva. La sfera osculatrice, con centro e raggio determinati dalla 0704222006 e 0704222007 rispettivamente ha contatto di terzo ordine con C.

In generale il piano osculatore è l’unico piano che ha contatto di secondo ordine con una curva.