indice

back to homepage

I principi della meccanica classica

Coordinate lagrangiane

Il lavoro virtuale e il principio di D’Alembert

Principio di D’Alembert per un sistema dinamico ed equazioni di Lagrange

Il principio della minima azione

 

 

i principi della meccanica classica

back to index

 

❍  Primo principio

In assenza di forze, ogni corpo isolato persevera nel suo stato di quiete o di moto rettilineo uniforme. Se definiamo la quantità di moto come il prodotto del vettore velocità per la massa si può scrivere:

 

p = m ⋅ v = k

 

dove k è una costante.

 

❍  Secondo principio

La variazione della quantità di moto di un corpo è proporzionale alla forza applicata ed avviene nella direzione e nel verso di tale forza. La forza viene implicitamente definita come la variazione della quantità di moto:

 

 

Se consideriamo la massa della particella come costante (ciò che è vero per velocità non relativistiche) possiamo scrivere:

 

m ⋅ a = F

 

dove a è il vettore che esprime la derivazione della velocità del corpo rispetto al tempo.

Tanto più grande è la massa della particella, tanto più piccola è l’accelerazione. La massa può dunque essere interpretata come il coefficiente di cambiamento della velocità di una particella a seguito della applicazione di una forza.

 

❍  Terzo principio

L’azione è sempre uguale alla reazione, ovvero le forze che due particelle esercitano l’una sull’altra hanno la direzione della linea che congiunge le due particelle, hanno lo stesso modulo e verso opposto.

 

Viene postulata l’esistenza di un sistema di riferimento in cui valgono i tre principi della meccanica, chiamato sistema inerziale.

Dalla legge di inerzia segue che qualsiasi sistema in moto relativo uniforme rispetto ad un sistema inerziale è a sua volta un sistema inerziale.

I due sistemi sono legati dalle trasformazioni di Galileo:

 

 

 

 

coordinate lagrangiane

back to index

 

Le coordinate cartesiane della particella sono due: x₁ e x₂, che costituiscono le componenti di un vettore posizione x(x₁ ,  x₂).

Se le particelle che costituiscono il sistema sono tutte libere si ha un sistema libero; altrimenti un sistema vincolato.

Si definiscono vincoli olonomi quelli che possono essere espressi nella forma:

 

f(x₁,x₂) = k

 

e cioè sotto forma di rapporti tra le coordinate della particella.

I vincoli che non possono essere espressi in tale forma sono detti vincoli anolonomi.

I sistemi soggetti a tali vincoli sono chiamati sistemi olonomi.

I vincoli sono visti come forze che agiscono sulle particelle limitandone la mobilità. Queste forze sono dette forze vincolari o reazioni vincolari. Le altre forze agenti che non derivano da vincoli sono dette forze attive.

L’analisi classica consideriamo sistemi inerziali.

Supponiamo di avere un sistema bidimensionale formato da una particella puntiforme di massa m che si muove lungo una curva ascendente di equazione x₂ = x₁² e che è sottoposta ad un campo gravitazionale uniforme i cui vettori sono paralleli all’asse y e con verso contrario.

Il vincolo del nostro esempio è un vincolo olonomo. Infatti, il vincolo risultante dal fatto che la particella si può muovere solo lungo la curva ascendente è esprimibile con la formula:

 

x₂ = x₁² + kt

 

e cioè:

 

–x₁² –kt + x₂ = 0

 

La presenza del vincolo fa sì che le coordinate cartesiane siano in realtà dipendenti l’una dall’altra: il sistema ha quindi non due, ma un grado di libertà.

Un modo più economico di esprimere la posizione della particella è quello di coordinatizzarla con coordinate indipendenti, che prendono il nome di coordinate generali o coordinate lagrangiane dal nome di J.L. de Lagrange, che le introdusse.

Non esiste un solo modo per scegliere le coordinate lagrangiane, ma piuttosto infiniti. Noi sceglieremo come coordinata lagrangiana il valore di x₁, dal quale si può immediatamente calcolare il valore di x₂.

Usualmente, per distinguere dalle coordinate cartesiane, indicate con x_i, le coordinate lagrangiane vengono indicate con q_i.

Poiché la particella è in movimento, le coordinate lagrangiane, come le coordinate cartesiane, sono funzioni di t, e andrebbero scritte come x₁(t) e q₁(t). In quanto tali esse possono essere derivate rispetto al tempo.

Esiste una precisa corrispondenza tra coordinate lagrangiane e coordinate cartesiane. Abbiamo dunque delle equazioni di trasformazioni di coordinate:

 

x₁ = x₁(q₁,…,q_n)

x₂ = x₂(q₁,…,q_n)

 

La jacobiana di questa trasformazione deve avere rango pari ai gradi di libertà.

Proseguendo nel nostro esempio, essendoci solo la coordinata q₁ scriviamo:

 

x₁ = x₁(q₁)

x₂ = x₂(q₁)

 

e cioè:

 

[0708091855]          x₁ = q₁

[0708091855]          x₂ = q₁² + kt

 

Il vincolo che abbiamo introdotto è un vincolo dipendente dal tempo, perché le espressioni mostrano che il piano inclinato si trasla in alto con moto uniforme.

Il sistema ha anche delle condizioni iniziali q₁⁰, x₁⁰, x₂⁰ che sono utilizzate per integrare le equazioni differenziali che esprimono e condizioni del sistema in un momento di tempo t qualsiasi.

Quando vi sono più particelle, con relative velocità, l’esposizione si limita alle equazioni della singola particella, in cui compare l’indice i per indicare appunto particella "i-esima", mentre per le coordinate lagrangiane si utilizza l’indice j.

Possiamo ora esprimere i vettori posizione delle particelle come funzioni delle coordinate lagrangiane e del tempo:

 

x₁ = x₁(q₁ , t)

x₂ = x₂(q₁ , t)

 

La presenza di t non significa altro che nelle [0708091855] il tempo compare come variabile. Questo indica una doppia dipendenza di x₂ dal tempo: in ogni tempo t il valore di q₁²(t) va modificato di una quantità dipendente direttamente dal tempo, che non è inglobata in q₁.

Niente impedisce di considerare come coordinata lagrangiana l’espressione x₁² + kt : in questo caso, terminologicamente, il vincolo non sarebbe dipendente dal tempo.

Supponiamo che la particella, sotto l’effetto della forza gravitazionale, sia in movimento. Possiamo calcolare il valore delle componenti x₁’ e x₂’ della velocità, ed esso risulta:

 

[0708061900]         

 

Essa non è altro che l’applicazione del chain rule o regola di derivazione delle funzione composte:

 

[0708091906]         

 

dove l’ultimo addendo si riduce chiaramente a ∂x/∂t

Possiamo considerare un esempio semplificato, lineare, che ci permette di interpretare meglio le derivate, in cui il vincolo sia una retta con pendenza +2 che si sposta verso l’alto. Allora si ha:

 

 

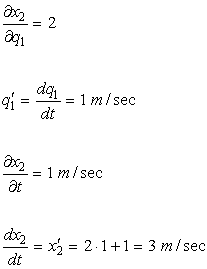
In questa formula le q_i′ sono dette velocità generalizzate.

 

 

 

il lavoro virtuale e il principio di d'alembert

back to index

 

Uno spostamento infinitesimo della particella in una qualsivoglia direzione produce ovviamente un lavoro, che è una quantità scalare data dal prodotto del modulo della forza per la componente dello spostamento lungo il vettore della forza. Per ottenere il lavoro occorre integrare lungo il percorso della particella il prodotto scalare del vettore forza per il vettore tangente al percorso.

In un sistema sottoposto a vincoli si definisce spostamento virtuale uno spostamento compatibile con i vincoli che, nel caso si tratti di vincoli dipendenti dal tempo, vengono tenuti fermi a partire dall'istante in cui inizia lo spostamento.

Si definisce spostamento reale uno spostamento compatibile con i vincoli ed il loro eventuale movimento.

Se si considera un sistema sottoposto a vincoli olonomi, gli spostamenti effettivi delle coordinate q_i e delle coordinate x_i sono legati dai rapporti:

 

[0708092113]          

 

mentre nel caso virtuale si ha la formula:

 

[0708092114]          

 

Ovviamente, se i vincoli non dipendono dal tempo, spostamento reale e spostamento virtuale coincidono, e si ha la [0708092114]   .

Per spostamenti infinitesimi si considera come se le forze cui è soggetta la particella non siano soggette a cambiamento.

Uno spostamento virtuale si dice spostamento reversibile o spostamento bilatero se anche il suo opposto è virtuale.

Poiché la particella è soggetta a forze, ad ogni spostamento virtuale corrisponde un lavoro virtuale, dato dalla formula:

 

[0708092119]          

 

dove le F_i sono le componenti nella direzione dello spostamento della forza attiva risultante che agisce sulla particella e le Φ_i sono le componenti nella direzione dello spostamento della forza reattiva risultante, e le δ_i sono le componenti dello spostamento.

Nel caso di un sistema sottoposto a vincoli senza attrito (vincoli lisci in cui la reazione vincolare è sempre normale al vincolo) si possono eliminare le forze reattive dalla [0708092119], perché (si consideri ad es. il caso della forza reattiva del piano inclinato) la forza reattiva è sempre normale allo spostamento vincolato e l'unico altro lavoro sarebbe il lavoro positivo compiuto dall'attrito.

Nel caso di un sistema con forze in equilibrio, poiché la componente forza per definizione è eguale a zero (e la forza non cambi a seguito dello spostamento della particella) il lavoro virtuale è zero

Nel caso in cui invece esista una forza attiva che agisce sulla particella (il che non vuol dire che la particella si muova, né che il sistema non possa essere in equilibrio: si consideri il caso di una perlina che è immobile sul fondo di una scodella, soggetta alla forza di gravità) si può constatare che il lavoro è negativo.

Si consideri un sistema in equilibrio soggetto a vincoli lisci; gli si dia uno spostamento virtuale; si calcoli il lavoro virtuale utilizzando la [0708092119].

In tale calcolo può essere trascurato il lavoro Φ ⋅ δx_i delle forze reattive, perché nel caso di vincoli lisci lo spostamento è sempre normale alla forza vincolare.

Il calcolo del lavoro virtuale si riduce quindi a:

 

[0708100551]          

 

e cioè al calcolo del lavoro virtuale delle forze attive.

Consideriamo l'esempio di un sistema in equilibrio costituito da una particella vincolata ad una superficie liscia (non necessariamente un piano) e calcoliamo il lavoro virtuale delle forze attive. Se consideriamo il moving frame of reference della particella nella direzione del moto possiamo considerare le componenti F_t, F_b, F_n della forza rispettivamente lungo la tangente, la normale e la binormale.

Si ha

 

F_b ⋅ δx_b = 0

 

perché δx_b è zero, in quanto spostamento non possibile perché normale alla superficie.

Le forze F_t e F_n devono essere pari a zero perché si verifichi la condizione di equilibrio, e quindi si ha pure

 

F_t ⋅ δx_t = 0

F_n ⋅ δx_n = 0

 

Come si vede, il lavoro virtuale delle forze attive è zero.

Consideriamo l'esempio di un sistema in equilibrio costituito da una particella che in un piano verticale è vincolata a rimanere all'interno di una circonferenza di raggio R (vale a dire che la particella può trovarsi in qualsiasi punto all'interno della circonferenza e non solo sulla circonferenza), sottoposta alla forza di gravità g.

L'unica posizione di equilibrio di tale sistema è quella con la particella localizzata all'intersezione del diametro verticale della circonferenza con la metà inferiore della stessa.

In questo caso possiamo considerare due tipi di spostamenti virtuali: spostamenti reversibili, tangenti alla circonferenza, e spostamenti non reversibili, in qualsiasi altra direzione: si consideri ad esempio lo spostamento verticale: se è possibile salire non è però possibile scendere, quindi lo spostamento opposto a quello ascendente non è possibile per la presenza del vincolo.

Se facciamo spostare la particella di una distanza infinitamente piccola lungo la linea tangente alla circonferenza (spostamento invertibile) otteniamo un lavoro virtuale nullo, perché lo spostamento è normale alla forza di gravità.

Se facciamo spostare la particella in verticale (spostamento non invertibile) otteniamo un lavoro virtuale negativo pari a

 

δx ⋅ m ⋅ g < 0

 

perché la particella si muove in senso inverso alla forza di gravità agente.

Se ribaltiamo il principio, imponendo al lavoro virtuale delle forze attive di essere inferiore o eguale a zero, si ha la condizione di equilibrio.

Il principio dei lavori virtuali o principio di D'Alembert stabilisce appunto che un sistema soggetto a vincoli lisci è in equilibrio se e solo se il lavoro virtuale delle forze attive non è mai positivo.

 

 

 

principio di d'alembert per un sistema dinamico ed equazioni di lagrange

back to index

 

Anche un sistema dinamico può essere analizzato in base al principio dei lavori virtuali: basta aggiungere alle forze attive le forze di inerzia, opposte ai prodotti delle masse per le accelerazioni.

In altre parole, ad ogni particella in moto si associ, oltre alla forza attiva, una forza, la forza d'inerzia, data da:

 

– m ⋅ a

 

Tale espressione è l'inverso di quella che compare nella:

 

[0708100636]          m ⋅ a = F + R

 

dove F sono le forze attive e R le forze reattive e che è la condizione che il sistema deve verificare in ogni momento. Per la [0708100636] possiamo quindi scrivere:

 

[0708100636]          F + R – m ⋅ a = 0

 

Tale equazione può essere interpretata come una condizione di equilibrio della particella, e quindi si può applicare il principio dei lavori virtuali nella forma:

 

[0708100638]          (F – m ⋅ a) ⋅ δx = 0

 

e cioè:

 

[0708100639]          F ⋅ δx  – m ⋅ a ⋅ δx = 0

 

 

dove nuovamente abbiamo eliminato le forze reattive.

Cerchiamo ora di esprimere la [0708100638] nei soli termini delle coordinate lagrangiane.

Lo spostamento δx in termini delle q_i può essere espresso come:

 

[0708100640]          

 

Definiamo poi Q_j come:

 

[0708100641]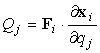          

 

Per le [0708100640] e [0708100641] possiamo scrivere il primo addendo della [0708100639] come:

 

[0708100642]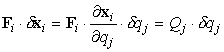          

 

Per quanto riguarda il secondo addendo della [0708100639], ricordiamo anzitutto che, avendo eliminato la mobilità dei vincoli, la variabile t sparisce dalla formula

 

[0708100737]         

 

Possiamo scrivere il secondo addendo della [0708100639] come:

 

[0708100643]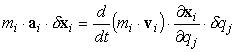          

 

Poiché è evidentemente:

 

[0708100741]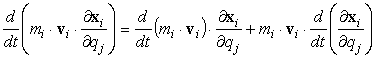          

 

allora, con una semplice manipolazione algebrica della [0708100741] si può scrivere:

 

[0708100742]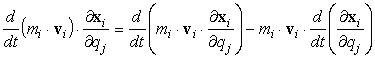          

 

e quindi il il secondo addendo della [0708100639] diviene:

 

[0708100743]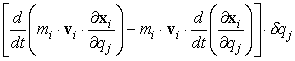          

 

Se consideriamo che è:

 

[0708100840]          

 

e che è:

 

[0708100842]          

 

e quindi:

 

[0708100843]          

 

e che perciò è:

 

[0708100841]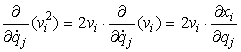          

 

allora possiamo scrivere il contenuto della prima parentesi tonda della [0708100743] come:

 

[0708100745]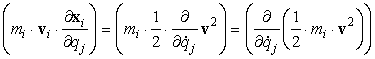          

 

Per quanto riguarda l'addendo con segno meno entro la parentesi quadra della [0708100743] si consideri anzitutto che è:

 

[0708100916]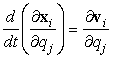          

 

Allora, poiché è:

 

[0708100918]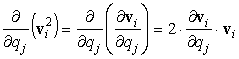          

 

si ha:

 

[0708100924]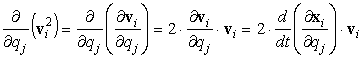          

 

Perciò possiamo scrivere l'addendo con segno meno come segue:

 

[0708100922]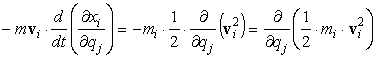          

 

Tutta la [0708100743] diviene dunque:

 

[0708100930]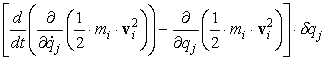          

 

Se indichiamo con  possiamo scrivere la [0708100930] nella forma:

 

[0708100934]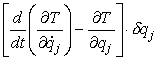          

 

Tenendo conto della [0708100934] e della [0708100641] la [0708100639], che esprime il principio di D'Alembert, diviene:

 

[0708100936]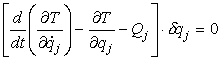          

 

Dalla [0708100936] ricaviamo immediatamente che deve essere:

 

[0708100939]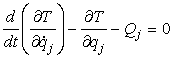          

 

e cioè:

 

[0708100941]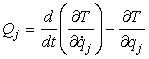          

 

Ipotizziamo ora che la forza agente sulla particella sia una forza gravitazionale.

Tali tipi di forze sono dette forze conservative, e sono legate alla esistenza di un campo scalare U (cioè di una funzione definita su R³), detto campo di potenziale con cui intrattengono la semplice relazione:

 

[0708101032]          F = – ∇U

 

dove ∇U indica il gradiente di U nel punto occupato dalla particella. L’energia potenziale U dipende solo dalle coordinate di posizione, e quindi in particolare dalle q_i e non dalle velocità generalizzate q_i′.

Se le forze attive agenti sono forze conservative allora nella [0708100941] si può sostituire la [0708101032] ottenendo:

 

[0708100942]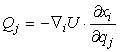          

 

Poiché  la variazione dx per una variazione unitaria di q_i è  e tale spostamento, moltiplicato scalarmente per le componenti del gradiente (cioè per le componenti della forza) dà un lavoro che rappresenta la variazione del potenziale U, possiamo scrivere:

 

[0708101034]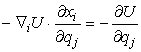          

 

e quindi:

 

[0708101035]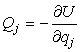          

 

Scriviamo ora la [0708100941] tenendo conto della [0708101035]:

 

[0708101043]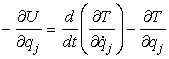          

 

da cui:

 

[0708101044]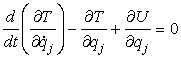          

 

da cui:

 

[0708101045]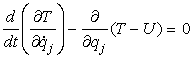          

 

da cui, tenendo presente che, poiché U non dipende dalle velocità q_i′, si ha  , e quindi tale termine può essere introdotto dove si vuole e col segno che si vuole:

 

[0708101046]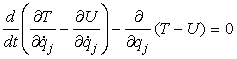          

 

da cui:

 

[0708101047]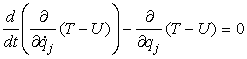          

 

Introduciamo ora la funzione lagrangiana o semplicemente lagrangiana del sistema, ponendo:

 

[0708101057]          L = L(q_j , q_j′, t) = T – U

 

La lagrangiana non è altro che la espressione delle energie cinetica T e potenziale U non in termini di x_j ma in termini di q_j calcolata in un sistema inerziale. Vedi più avanti esempi di calcolo della lagrangiana.

Tenendo presente la lagrangiana, la [0708101047] diviene:

 

[0708101049]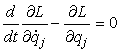          

 

che prende il nome di (i-esima) equazione di Lagrange.

 

 

 

il principio della minima azione

back to index

 

La descrizione lagrangiana di un sistema meccanico è alquanto differente da quella newtoniana. Non ci si focalizza sulla evoluzione del sistema a partire da condizioni date, ma sulla evoluzione del sistema tra due momenti di tempo t₁ e t₂ separati da un intervallo infinitesimo.

La descrizione lagrangiana mostra che in tale intervallo di tempo il sistema muta in modo da minimizzare il valore dell’integrale:

 

[0708101308]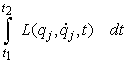          

 

dove L è appunto la lagrangiana relativa alla i-esima particella.

Il valore dell’integrale [0708101308] è chiamato la azione corrispondente ad una particolare traiettoria q_i(t) seguita dalla i-esima particella. Si parla in proposito di principio di minima azione.

Usando il calcolo delle variazioni la condizione che un dato integrale abbia un minimo sulla funzione q_j(t) è trasformato in una equazione differenziale per q_j(t). Se la lagrangiana è scelta correttamente, il principio della minima azione si traduce in equazioni differenziali che sono equivalenti alle corrette equazioni newtoniane per forza e accelerazione.