I matematici utilizzano sovente quello che viene chiamato “metodo astratto”, per definire degli oggetti matematici che hanno alcune caratteristiche degli oggetti della nostra esperienza, ma per il resto se ne discostano. Come è stato detto, un simile atteggiamento può essere riassunto nel motto: l’oggetto matematico è quel che fa.

Questo è particolarmente vero nella geometria a più di tre dimensioni.

La geometria a più di tre dimensioni. Lo spazio a più di tre dimensioni. Punto dello spazio a più di tre dimensioni.

back to index

Un ottimo esempio di metodo astratto è fornito dalla geometria moderna: uno studente che apra un testo universitario di Geometria aspettandosi di trovare figure simili a quelle che illustravano i teoremi di Euclide nei libri su cui egli ha studiato sin dalle elementari troverà un testo senza alcuna illustrazione, pieno di definizioni assiomatiche e di simboli appartenenti all’algebra astratta.

Questo è il prezzo che si paga per una grande generalizzazione delle nozioni geometriche, che consente di applicarle con profitto a tutti i rami delle scienze fisiche, naturali e all’ingegneria.

In questo campo, da tempo i matematici hanno abbandonato la limitazione costituita dalle tre dimensioni; anzi si può dire che la matematica avanzata si occupa principalmente di oggetti di dimensione superiore a tre.

Questo può risultare sconcertante: un solido può essere visualizzato in tre dimensioni e una superficie in due dimensioni, ma cos’è una sfera quadridimensionale?

La fisica einsteniana suggerisce che la quarta dimensione possa essere il tempo, e che quindi lo spazio in cui viviamo è in realtà uno spazio-tempo quadridimensionale chiamato cronotopo. Ma quando si va a tracciare linee e superfici in questo spaziotempo si cozza pur sempre col problema della non intuitività di tali nozioni. Inoltre, le geometrie più interessanti sono quelle con un numero molto elevato di dimensioni. La geometria a sei dimensioni, per esempio, è molto interessante perché consente di descrivere il moto di una particella nello spazio.

In geometria superiore (i termini geometria astratta o geometria moderna sono egualmente eloquenti) vengono definite delle proprietà e null’altro che delle proprietà, che vengono attribuite a qualcosa che ha un nome e gode di tali proprietà. Null’altro è richiesto. Ad esempio, al nome di “spazio vettoriale quadridimensionale” corrisponde l’idea di un insieme di elementi non meglio specificati chiamati “punti” che godono della proprietà di essere addizionati e moltiplicati per un numero reale e ciascuno dei quali può essere espresso come somma di multipli di non più di quattro vettori indipendenti chiamati “vettori base”.

Lo spazio vettoriale non ha niente a che spartire con lo spazio fisico, e non solo per il numero di dimensioni: mentre nello spazio fisico possiamo esprimere la distanza tra due punti, nello spazio vettoriale non esistono distanze. Mentre nello spazio fisico possiamo, a partire da un punto che fa da centro, visualizzare i punti come insiemi racchiusi in sfere aventi centro in tale punto, e definire per tal via in modo rudimentale una “posizione reciproca” dei punti, niente di simile può essere fatto per lo spazio vettoriale, a meno di non dotarlo di una struttura ulteriore, chiamata “topologia naturale”.

Riguardo le proprietà dell’oggetto i matematici richiedono solamente che esse non siano contraddittorie. Si può perfettamente concepire il personaggio di un racconto come coraggioso, di sesso maschile, generoso e via dicendo, con l’unico limite che le sue qualità non devono contraddirsi: la compassione non può accompagnarsi alla crudeltà e l’intelligenza e l’accortezza non possono accompagnarsi alla propensione a compiere atti sciocchi.

Se stabilire proprietà arbitrarie per un oggetto può essere divertente e svincolare la creatività dai limiti della esperienza fisica, però può talvolta essere di scarso interesse quando tali proprietà non abbiano nessuna remota attinenza col nostromondo quotidiano; il metodo astratto è così chiamato proprio perché astrae da un oggetto della esperienza delle qualità o caratteristiche, liberandole dal collegamento con altre caratteristiche o da alcune limitazioni che ad esse impone l’esperienza. Un ottimo esempio è il concetto matematico di spazio.

Uno spazio fisico ha una dimensione, e ugualmente la avrà uno spazio astratto, ma mentre le dimensioni dello spazio fisico sono tre, definite come la possibilità di misurare, a partire da un punto, distanze lungo tre assi mutuamente ortogonali, uno spazio astratto può avere milioni di dimensioni e persino infinite dimensioni, definite come la quantità di numeri occorrente per distinguere due punti in tale spazio. Così facendo, abbiamo utilizzato un concetto noto, quello di rappresentazione cartesiana, che attribuisce ad un punto la terna di numeri chiamati coordinate e costituiti dalle sue distanze con segno da tre assi, e ne abbiamo astratto l’idea-base: quella di un punto definito da una enopla di numeri che è sufficiente a distinguerlo da un altro punto. Viene abbandonato ogni riferimento ad operazioni di misurazioni o distanze, e in molti testi di matematica viene fatto il passo ulteriore di identificare il punto con la enopla di numeri. Ma questa ulteriore astrazione non è strettamente necessaria e sebbene porti vantaggi in certe trattazioni avanzate, può generare qualche confusione nel lettore senza sufficiente dimestichezza con l’algebra lineare moderna.

Nella figura 0705161732 è mostrato il procedimento di coordinatizzazione di uno spazio bidimensionale mediante rappresentazione cartesiana:

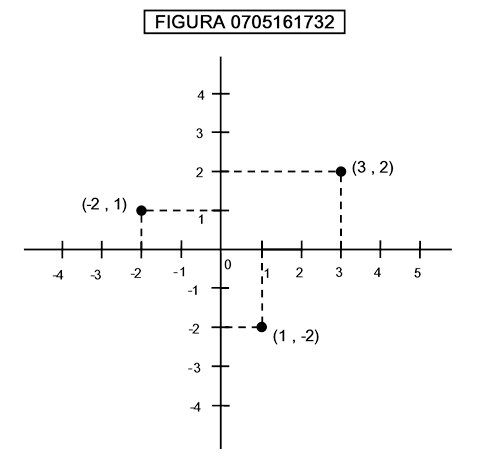
Le coppie di numeri accanto a ciascun punto sono le distanze con segno dagli assi.

Si noti che la attribuzione di coppie di valori è largamente arbitraria: possiamo ruotare gli assi ottenendo nuove coordinate; così come possiamo passare ad una classe più vasta di rappresentazioni chiamate rappresentazioni affini dello spazio, esemplificate nella figura 0711110959:

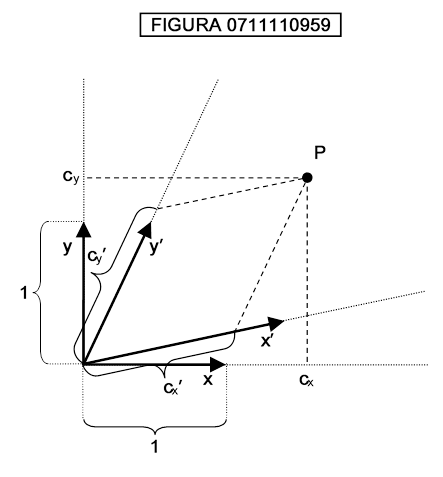
Si vede da tale figura che le coordinate del punto P, che avendo come riferimento gli assi cartesiani ortogonali x,y sono cx e cy, prendendo come riferimento il sistema di riferimento affine x′ e y′ diventano cx′ e cy′.

La nozione di spazio pluridimensionale è oggi correntemente accettata senza discussioni e impiegata con profitto proprio nella spiegazione del mondo fisico. Le recenti teorie delle stringhe parlano di universi di dieci dimensioni in cui oggetti apparentemente tridimensionali come le particelle subatomiche avrebbero in realtà sei dimensioni aggiuntive rappresentabili come stringhe che vibrano e che spiegano il loro comportamento negli acceleratori dei laboratori.

Quando si ha a che fare con un numero di dimensioni superiori a tre cambia il modo di scrivere le formule.

Si usano x₁, x₂,…, x_n anziché le tradizionali x, y, z, w… per le variabili e per le costanti si scrive a₁, a₂, …, a_n (b₁, b₂,…b_n ecc.) invece delle tradizionali a, b, c,…

Così, una espressione che lo studente è abituato a scrivere come:

ax + by + cz = 0

diviene:

a₁x₁ + a₂x₂ + a₃x₃ = 0

Cambia anche il modo di scrivere le somme. Lo studente avrà già appreso, invece di:

a₁x₁ + … + a_nx_n

a scrivere:

Quando si ha a che fare con complesse espressioni riguardanti gli iperspazi, si ricorre ad una ulteriore semplificazione e si scrive semplicemente:

a_ix_i

convenendosi (convenzione di Einstein, che fu il primo ad introdurla) che due indici identici di due simboli moltiplicati implicano una somma per ogni valore dell’indice.

Dimensioni e sottospazi

back to index

Il numero di coordinate necessarie per individuare un punto dello spazio esprime quella che si chiama la dimensione di uno spazio.

Come avrà notato lo studente, in matematica superiore la parola “spazio” è utilizzata per indicare non solo lo spazio tridimensionale, ma spazi di qualsiasi dimensione. Così, secondo questa terminologia, un punto è uno spazio zerodimensionale (o, come si dice, 0-spazio); una linea è uno spazio monodimensionale o spazio 1-dimensionale o 1-spazio; un piano è uno spazio bidimensionale o spazio 2-dimensionale o 2-spazio; lo spazio fisico in cui viviamo come descritto dalla geometria euclidea studiata a scuola è uno spazio tridimensionale o spazio 3-dimensionale o 3-spazio.

Ogni spazio ha dei sottospazi, che sono precisamente gli spazi di dimensione minore in esso immersi. Così, gli unici sottospazi della linea sono i punti; i sottospazi del piano sono le linee e i punti; i sottospazi dello spazio tridimensionale sono i punti, le linee, i piani; e così via per gli spazi di dimensione superiore..

Semispazio è una delle due parti in cui un iperpiano divide uno spazio, insieme all’iperpiano stesso

Generalizzazione del concetto di distanza euclidea

back to index

Qual è la definizione di “distanza” in uno spazio con più di tre dimensioni? La figura 0705161738 mostra come in uno spazio bidimensionale, ad ogni coppia di punti, P,Q oppure R,Q oppure P,R può essere associato un numero detto distanza.

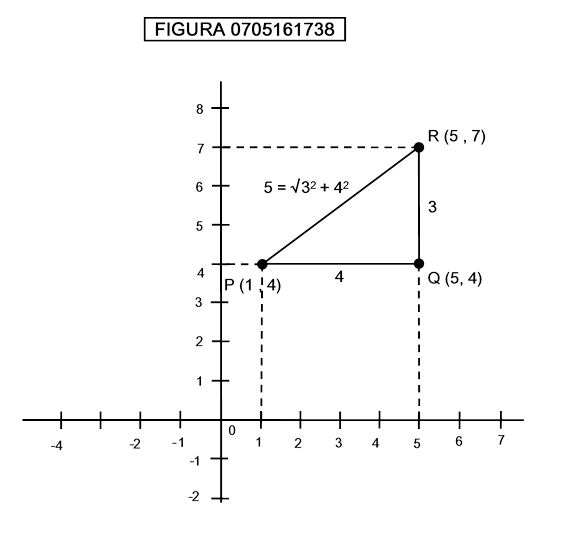
La distanza tra P e Q, è calcolata semplicemente facendo la differenza tra il valore della coordinata x di Q e la coordinata x di P; la distanza tra Q ed R è calcolata facendo la differenza tra le coordinate y, mentre la distanza tra P ed R è calcolata a partire dalle distanze PQ e QR utilizzando il teorema di Pitagora:

Un ragionamento analogo ma leggermente più complicato vale in tre dimensioni e mostra che la distanza tra due punti T di coordinate (a,b,c) e V di coordinate (d,e,f) è:

Ci accorgiamo subito che in tutti i casi, compresi quelli della distanza PQ e QR, si è applicata la stessa formula, chiamata la formula pitagorica della distanza o, più frequentemente, formula della distanza euclidea:

dove x_p1 e x_p2 sono le coordinate x rispettivamente del primo e del secondo punto e y_p1 e y_p2 sono le coordinate y rispettivamente del primo e del secondo punto.

Una simile formula può essere facilmente generalizzata ad n dimensioni:

dove abbiamo impiegato i simboli x₁^k per indicare la k-esima coordinata del primo punto p₁ e i simboli x₂^k per indicare la k-esima coordinata del secondo punto p₂

Tale formula viene usualmente definita come la formula della distanza euclidea per spazi multidimensionali.

Per esempio, la distanza tra i due punti (1,0,-1,4,2) e (3,1,1,1,-1) (che stanno nello spazio a cinque dimensioni) è:

E se questa vi sembra una generalizzazione ardita del concetto di distanza, dovete sapere che i matematici non si sono fermati qui, e hanno definito la distanza non riemanniana mediante la formula del tensore metrico:

dove i valori:

dxⁱ = x₂ⁱ – x₁ⁱ

sono le differenze tra le i-esime coordinate, e dove i numeri g_jk fanno parte di una matrice arbitraria di valori.

Lo stesso Riemann ipotizzò una distanza data dalla radice quarta di una formula ogni addendo della quale è dato dalla moltiplicazione di quattro fattori.

In altre parole, nella geometria superiore degli iperspazi il concetto di distanza non è unico e connaturato allo spazio che si studia, ma è definito, e ad ogni definizione corrisponde uno spazio diverso, con caratteristiche uniche e peculiari che possono differire radicalmente da quelle dello spazio euclideo.

Generalizzazione del concetto di sfera

back to index

Avere generalizzato il concetto di distanza, possiamo generalizzare quello di sfera, definendola come l’insieme di punti di un iperspazio che hanno una distanza determinata da un punto chiamato centro.

Ad esempio, una sfera di raggio 10 e centro nel punto di coordinate (1,1,0,0,0) in uno spazio a 5 dimensioni dotato di distanza euclidea sarà data da tutti i punti P(x¹,x²,x³,x⁴,x⁵) le cui coordinate soddisfano la relazione:

Il concetto di ipersfera comprende quello di cerchio in uno spazio bidimensionale come il piano (detto S₁ o 1-sfera, perché occorre un solo parametro per coordinatizzarne i punti), di sfera vera e propria nello spazio tridimensionale (S₂ o 2-sfera), di sfera di dimensione 3 in uno spazio quadridimensionale (S₃ o 3-sfera) ecc.

Così come la sfera a 3 dimensioni ha una superficie bidimensionale, la sfera a 4 dimensioni ha come superficie uno spazio tridimensionale

Generalizzazione del concetto di cubo

back to index

Mediante la definizione di distanza possiamo anche generalizzare il concetto di cubo.

Come è noto, dati quattro vertici di un cubo, ne risultano definiti tutti gli altri: così, se i vertici sono (0,0,0), (3,0,0), (0,3,0), (0,0,3) gli altri vertici saranno costituiti da tutte le combinazioni possibili delle coordinate: (3,0,3), (3,3,0), (3,3,3), (0,3,3). Si veda la figura 0711111127.

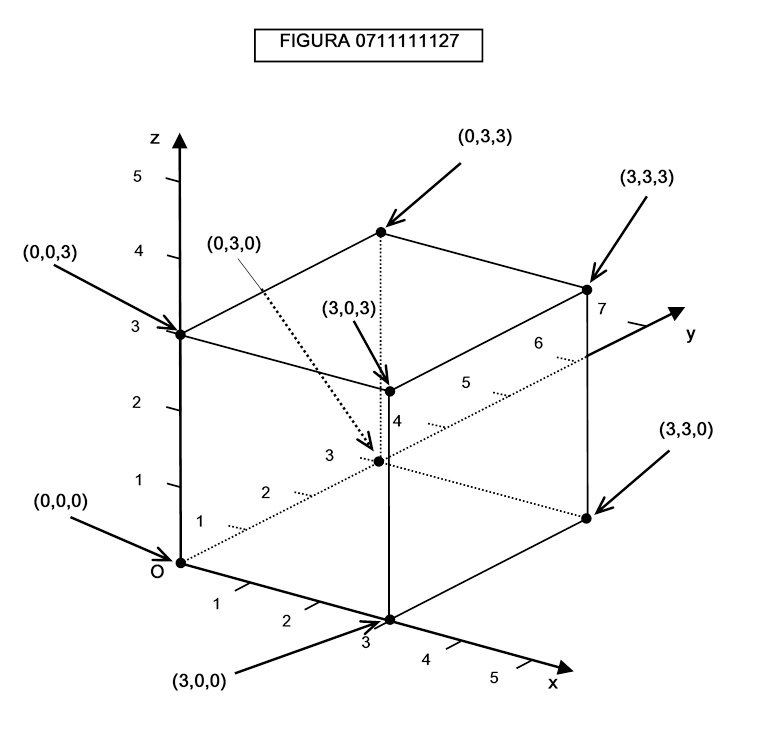
In questo modo possiamo ottenere tutti i vertici di un ipercubo di quattro dimensioni: essi saranno 64.

Per ogni dimensione dello spazio a cui appartiene l’ipercubo, otteniamo quindi due valori: la coordinata x¹ può assumere i valori 0 o 3; e così pure, nel nostro esempio, le altre coordinate.

E’ ora facile definire un ipercubo: i punti dell’ipercubo saranno quelli le cui coordinate sono comprese tra questi valori minimi e massimi.

Possiamo anche fare il conto degli spigoli, senza preoccuparci di farci una idea intuitiva di cosa essi siano; poiché in uno spazio tridimensionale da ogni vertice si diparte un numero di spigoli pari alla dimensione dello spazio, il numero degli spigoli di un cubo tridimensionale sembrerebbe pari a 8 ⋅ 3; in realtà abbiamo contato gli spigoli due volte, perché ad ogni spigolo che parte da un punto corrisponde uno spigolo che parte dal punto opposto. Pertanto il numero di spigoli di un generico ipercubo sarà dato da:

(numero vertici x numero dimensioni)/2

Generalizzazione del concetto di piano

back to index

Per generalizzare la nozioni di piano, consideriamo che l’equazione di un piano in tre dimensioni è data da:

[0705210652] ax + by + cz = 0

se il piano passa per l’origine (infatti in tal caso, se x = 0 e y = 0 deve essere z = 0) oppure da:

ax + by + cz = d

se il piano non passa per l’origine. Appare naturale allora, in uno spazio quadridimensionale, scrivere:

ax₁ + bx₂ + cx₃ + dx₄ = e

In uno spazio pentadimensionale possiamo scrivere:

ax₁ + bx₂ + cx₃ + dx₄ + ex₅ = f

In tal modo definiamo, per ogni spazio n-dimensionale, un insieme di punti che i matematici definiscono iperpiano. Esso ha la caratteristica tipica del piano tridimensionale della geometria euclidea: i punti di una iperlinea che ha due punti di contatto con esso, giacciono tutti su esso.

Esso ha anche un’altra caratteristica: può essere definito da un numero di parametri inferiore di uno alla dimensione dello spazio in cui si trova. Ad esempio, data l’equazione [0705210652] di un qualsiasi piano in uno spazio tridimensionale, vediamo che dando valori arbitrari a due delle coordinate variabili x,y la terza coordinata rimane univocamente fissata. Pertanto, per individuare un punto di un piano abbiamo bisogno di due valori: uno meno della dimensione dello spazio in cui il piano si trova (tre).

In altre parole, possiamo ottenere una rappresentazione parametrica:

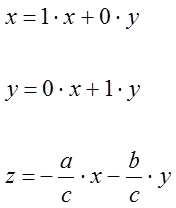
basata su due soli parametri.

Lo stesso è vero in dimensioni maggiori: un punto su un iperpiano di uno spazio a 4 dimensioni è individuato da 3 parametri, ecc.

iperspazi non euclidei

Spazi euclidei e spazi non euclidei

back to index

Quelli di cui abbiamo parlato finora sono spazi pluridimensionali euclidei, che generalizzano l’unico tipo di spazio che lo studente di scuola media superiore conosce – quello bidimensionale o tridimensionale della geometria euclidea e quello bidimensionale dell’analisi delle funzioni di una variabile reale.

Ma la geometria avanzata conosce svariati tipi di spazi pluridimensionali: spazi vettoriali, spazi affini, spazi proiettivi, spazi di Riemann, solo per citare i primi che si incontrano approfondendo lo studio della disciplina.

Prima di arrivare a parlare di tali spazi, definiti spazi astratti, introduciamo un esempio che ci servirà per chiarire le idee: lo spazio delle fasi di una bicicletta.

Lo spazio delle fasi di una bicicletta

back to index

Una bicicletta ha cinque parti mobili: il manubrio, la ruota anteriore, l’insieme pedivella-catena-ruota posteriore e i pedali (figura 0705251106) Ognuna di queste parti richiede, per la sua descrizione, una coordinata di posizione e una coordinata di velocità. Il movimento di una bicicletta, se non consideriamo la sua posizione sulla strada, è quindi il moto in uno spazio a dieci dimensioni. Un tale tipo di spazio, che ha dimensioni che rappresentano posizioni e dimensioni che rappresentano velocità prende il nome di spazio delle fasi.

Gli spazi astratti della matematica moderna

back to index

Dall’esempio precedente (spazio delle fasi di una bicicletta) cominciamo a renderci conto che la matematica moderna utilizza spazi in cui una o più delle caratteristiche che usualmente associamo al concetto di “spazio” può mancare.

Può scomparire il concetto di distanza: nello spazio delle fasi della bicicletta, che distanza ci può essere tra una bici col manubrio voltato a destra e una bici col manubrio voltato a sinistra?

Può essere definita una distanza del tutto differente da quella euclidea, come nel caso del cronotopo (spaziotempo) della relatività ristretta.

Per quanto sia difficile crederlo, esistono spazi in cui è definita la posizione reciproca dei punti ma in cui non può essere definita una distanza, nel senso che qualsiasi funzione distanza che fosse definita darebbe una topologia diversa da quella considerata.

Questi spazi differenti dallo spazio euclideo ricadono entro categorie generali aventi caratteri comuni. Spesso i matematici non sono interessati allo studio di questo o quello spazio particolare, ma precisamente di queste categorie, definite come spazi astratti.

Uno spazio astratto è un insieme di punti dotato di una struttura generalmente definita specificando un insieme di assiomi che devono essere soddisfatti dai punti.

Si tratta di un tipico approccio assiomatico: esattamente come nella geometria euclidea, il concetto di “punto” è un concetto primitivo che resta non-definito, o meglio, viene definito solo attraverso le relazioni che ha con gli altri punti o con altri concetti primitivi.

Importanti tipi di spazi astratti sono lo spazio vettoriale, lo spazio topologico, lo spazio metrico, lo spazio di Hilbert.

Lo spazio vettoriale è uno spazio astratto, dove i punti o “vettori” u, v, w,… sono enti di qualsiasi genere che soddisfano i seguenti assiomi:

▸ u + (v + w) = (u + v) + w

▸ u + v = v + u

▸ Esistenza di un elemento tale che v + 0 = v

▸ 1 ⋅ v = v

▸ h ⋅ (k ⋅ v) = (h ⋅ k) ⋅ v

▸ k ⋅ (v + w ) = k ⋅ v + k ⋅ w

dove h, k sono numeri reali o complessi o elementi di strutture analoghe, chiamate campi e 1 è l’elemento neutro del campo.

Un esempio familiare di spazio vettoriale è lo spazio dei vettori liberi tridimensionali della fisica, che possiamo raffigurare come una “palla” irta di vettori che hanno il loro punto iniziale (o punto di applicazione) in una origine comune. Le copie di tali vettori applicate a questo o quel punto dello spazio, definiti vettori applicati, rappresentano in realtà un unico vettore libero, di cui hanno la stessa direzione, lo stesso verso e la stesso modulo o grandezza (lunghezza)

Un altro esempio, meno intuitivo, di spazio vettoriale, è quello delle enople di numeri con l’addizione componente per componente e la moltiplicazione scalare.

Esiste lo spazio vettoriale delle funzioni su insiemi (es. spazio di Banach), lo spazio vettoriale dei polinomi in x, lo spazio vettoriale delle matrici ecc.

Gli spazi metrici, come vedremo più avanti, sono insiemi tra due punti qualsiasi dei quali è stabilita una distanza. Negli spazi vettoriali metrici, dove esiste una distanza, vengono anche definiti angoli.

Gli spazio topologici, che pure vedremo, hanno definita la posizione reciproca dei punti ma non la distanza.

Anche lo spazio euclideo è in realtà studiato come spazio astratto, di cui lo spazio fisico è solo un caso particolare: i suoi “punti” possono essere qualsiasi cosa, dai polinomi alle matrici, ai punti dello spazio fisico ai vettori geometrici. La definizione matematica di spazio euclideo varia lievemente ma coincide nella sostanza: si tratta di uno spazio affine dotato di una metrica euclidea per alcuni matematici; per altri può essere descritto come lo spazio vettoriale delle enople (spazio prodotto di R) dotato di struttura di spazio affine e di distanza euclidea.

Queste due definizioni coincidono, se si considera che uno spazio vettoriale può essere pensato come spazio euclideo se si considerano i vettori come “punti” e i vettori-differenza tra due vettori dati come “vettori” di uno spazio euclideo. Ad esempio, il vettore differenza tra (3,3,3) e (1,1,1) è (2,2,2), che viene considerato come il vettore il cui capo iniziale è nel punto (2,2,2) e il cui capo finale è nel punto (3,3,3)

Parecchi degli “spazi” sopra descritti non hanno più molto in comune col concetto di spazio fisico cui siamo abituati: a parte il fatto di essere composti da “punti” a ciascuno dei quali possiamo assegnare una coordinata.

Spazi di Hilbert

back to index

Matematicamente, lo spazio euclideo appartiene alla importante categoria degli spazi di Hilbert. Leggiamo le parole con cui il matematico Tim Gowers lo definisce.

“Ma che cos’è uno spazio di Hilbert? Nei corsi universitari di matematica esso viene definito come uno spazio vettoriale completo dotato di prodotto interno. Si suppone che gli studenti che seguono le lezioni sappiano, dai corsi precedenti, che uno spazio è completo se in esso ogni successione di Cauchy è convergente. Naturalmente, per dare un senso a questa definizione, gli studenti devono conoscere anche le definizioni di spazio vettoriale, prodotto interno, successione di Cauchy e convergenza. Eccone almeno una (non la più lunga): una successone di Cauchy è una successione x₁, x₂, x₃,… tale che per ogni numero intero positivo ε, esiste un intero N tale che, per ogni coppia di interi p,q maggiori di N, la distanza tra x_p e x_q è minore di ε. In poche parole, per avere qualche speranza di capire cos’è uno spazio di Hilbert occorre prima studiare e digerire una lunga sequela di concetti di livello inferiore. Non stupisce che questo richieda tempo e fatica. E poiché lo stesso vale per molte delle più importanti nozioni matematiche, ciò pone limiti ben precisi agli argomenti trattabili in modo soddisfacente in una esposizione divulgativa della matematica attuale”.

Lo spazio delle posizioni di un’asta rigida su un piano

back to index

Supponiamo di avere un’asta rigida che può scivolare su un piano. La sua posizione (o configurazione ) può essere fissata assegnando le coordinate cartesiane x,y di una estremità e l’angolo θ che l’asta forma con una direzione prefissata. In questo caso lo spazio delle configurazioni è tridimensionale

Lo spazio che rappresenta il moto di un punto

back to index

L’utilità della geometria a più dimensioni consiste ad esempio nella straordinaria precisione con cui ci consente di descrivere delle configurazioni di oggetti fisici o di sistemi complessi, come ad es. quelli sociali o biologici

Di fatto anche la geometria in due e tre dimensioni è utilizzata per scopi che vanno oltre la semplice rappresentazione dello spazio fisico. Spesso, per esempio, rappresentiamo il moto di un oggetto tracciando un grafico che riporta le distanze percorse a tempi diversi.

Il piano in cui viene rappresentato il moto non ha esistenza fisica – è uno spazio delle fasi bidimensionale – e il moto dell’oggetto è un insieme di punti in tale spazio.

Più in generale la geometria multidimensionale aiuta a visualizzare e trattare problemi di meccanica, psicologia, economia, in cui intervenga un certo numero di variabili.

Lo spazio delle posizioni di una zolletta di zucchero su un tavolo

back to index

La posizione di una zolletta di zucchero che può essere spostata sul piano di un tavolo senza cambiare la faccia rivolta in basso può essere descritta fornendo le coordinate di due degli spigoli della faccia a contatto col tavolo. Poiché ogni spigolo ha due coordinate, una posizione della zolletta non è altro che un punto in uno spazio quadridimensionale. Si potrebbe pensare che ad ogni punto di tale spazio corrisponda una posizione della zolletta, ma non è così.

I due spigoli devono mantenere una distanza fissa. Supponendo che tale distanza sia di 2 cm le posizioni della zolletta saranno i punti dello spazio 4-dimensionale che soddisfano l’equazione:

si tratta di una equazione di secondo grado in quattro variabili, che definisce una ipersuperficie nel nostro spazio. In altre parole, le posizioni della zolletta possono essere visualizzate come una superficie in uno spazio quadridimensionale.

Lo spazio delle fasi del pendolo

back to index

Un pendolo è definito dalla sua posizione e dalla sua velocità. La posizione può essere espressa da un numero che individua un punto sulla circonferenza che esso può percorrere; la velocità può pure essere espressa con un singolo numero. Pertanto lo spazio delle fasi del pendolo è uno spazio bidimensionale.

Supponiamo che il pendolo, a cui è impressa una velocità iniziale v₀ dal suo punto di riposo, continui a muoversi indefinitamente senza attrito, sotto l’influenza dell’impulso iniziale e della forza di gravità.

Ad ogni velocità iniziale v₀ corrisponde una linea nello spazio delle fasi che descrive il moto del pendolo. Osserviamo tali linee nella figura 0705271234:

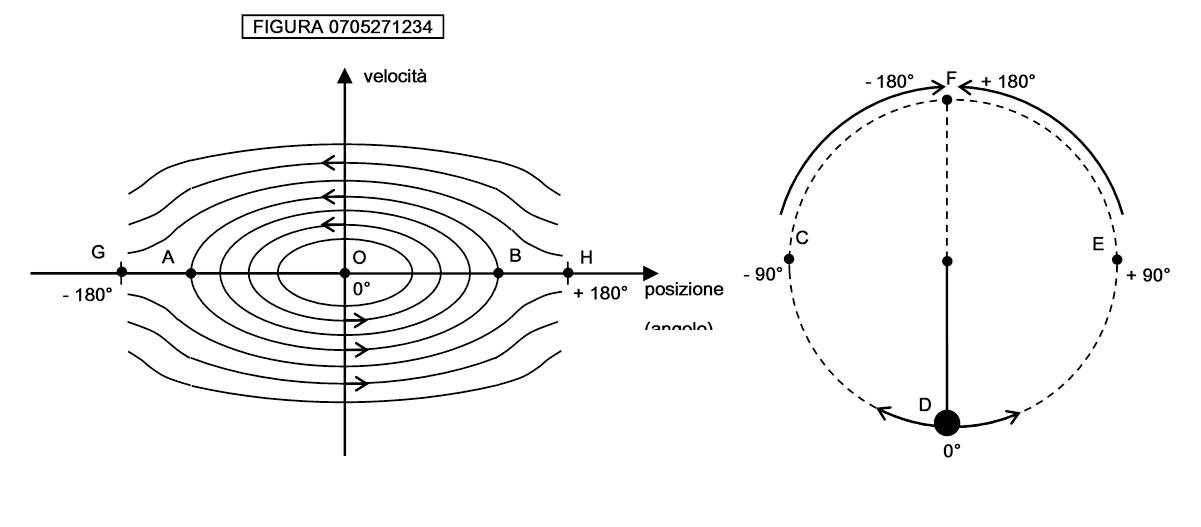
Se il pendolo è immobile la sua “traiettoria” consisterà di un punto singolo: il punto O è la posizione di equilibrio stabile del pendolo con il peso verso il basso, mentre i punti coincidenti G e H sono la posizione di equilibrio instabile del pendolo capovolto, col peso posto sopra l’asta.

Le linee chiuse sono le oscillazioni del pendolo che non ha sufficiente velocità per raggiungere il punto di svolta superiore F nella figura di destra e superarlo (traiettorie DEED della figura di destra)

Le linee aperte sono le traiettorie del pendolo che ha sufficiente velocità per arrivare al punto F e scendere dal lato opposto (traiettorie DEFCD della figura di destra).

Il cronotopo di Minkowski

back to index

Un esempio di spazio pluridimensionale è il cronotopo di Minkowski, uno spazio in cui la quarta dimensione è una coordinata legata al tempo t ed espressa, per ragioni di convenienza matematica come:

[0705280722] x⁴ = – i ⋅ c ⋅ t

Grazie alla forma matematica data alla coordinata x₄, dove i è l’unità immaginaria dei numeri complessi, un fronte d’onda luminosa che si espande ha equazione

[0705280723] x₁² + x₂² + x₃² + x₄² = 0

Se interpretiamo l’espressione a primo membro della [0705280724] come la distanza dei punti del fronte d’onda dall’origine possiamo introdurre la distanza relativistica:

[0705280724] x₁² + x₂² + x₃² + x₄²

Questa distanza ha un comportamento particolare: i punti del fronte d’onda di luce nello spaziotempo hanno distanza zero dall’origine. Distanze maggiori di quella relativistica tra due punti indicano che si sta prendendo in considerazione due eventi nello spaziotempo separati da una distanza spaziale superiore a quella che coprirebbe il raggio luminoso generato dal primo evento. Distanze minori di quella relativistica indicano che il secondo evento si verifica in un punto dello spazio che il raggio luminoso generato dal primo raggiunge prima che esso si verifichi.

In figura 0705280603 è mostrata la proiezione in tre dimensioni, x, y, t, di un ipercono che rappresenta il fronte d’onda di un lampo di luce che si diparte dal centro (0,0,0,0) del cronotopo. Il trucco che ci consente di visualizzarlo consiste nel rimuovere la dimensione z, come se si stesse guardando il cono di luce che si allarga sul “pavimento” costituito dal piano x, y quando accendiamo una lampadina. Allora ogni “foglio” orizzontale del grafico più in alto rappresenterà il cerchio di luce sul pavimento in momenti diversi.

Considerando la distanza relativistica come un invariante per trasformazioni lineari di coordinate si ottiene il gruppo di trasformazioni di Lorentz, che è l’espressione einsteiniana della relazione tra le coordinate di due sistemi inerziali.

Lo spazio delle variabili di un sistema economico

back to index

Gli economisti studiano il comportamento di sistemi economici con migliaia di operatori (consumatori e imprese) e decine di parametri che ne definiscono il comportamento (preferenze, età, reddito, consumi ecc. delle famiglie; quantità impiegata di fattori, produzione, profitti ecc. delle imprese).

In particolare, essi tentano di aiutare i manager a massimizzare i profitti agendo su centinaia di variabili (quantità di fattori impiegati, curve di domanda dei consumatori, costo dei fattori, spese di marketing ecc.). Pertanto lavorano in uno spazio a migliaia di dimensioni, dove i vincoli vengono visualizzati sotto forma di superfici multidimensionali come “ellissoidi ad n dimensioni” ed altri oggetti altrettanto esotici.

Le coordinate lagrangiane

back to index

L’esempio della zolletta di zucchero mostra anche come le “coordinate” di un sistema fisico descritto da uno spazio delle fasi normalmente siano “coordinate lagrangiane”.

Questo tipo di coordinate, fu introdotto nel Settecento dal grande matematico piemontese Jean-Louis de Lagrange nella sua opera Mécanique Analitique, che costituì il più grande avanzamento nello studio della meccanica dopo quello avutosi con Isaac Newton.

In uno spazio delle fasi ciò che conta è il numero dei gradi di libertà, cioè il numero di parametri necessari per descrivere uno stato del sistema. Come si è visto nel caso della zolletta, sovente le coordinate sono legate fra loro (dati due spigoli della zolletta, le coordinate degli spigoli rimanenti risultano deducibili da questi), in modo che un insieme di m velocità e posizioni può essere descritto con un numero n < m di parametri, corrispondenti ai gradi di libertà del sistema. Più vincoli ha un sistema (nel nostro esempio il vincolo consiste nella distanza tra gli spigoli della zolletta), minore è il numero dei parametri con cui può essere descritto. Ad esempio, la posizione della zolletta è completamente determinata dalla posizione di un vertice e dall’angolo che uno spigolo fissato della zolletta forma con tale vertice: la presenza del vincolo riduce a tre il numero dei parametri necessari per descrivere la sua posizione.

Il passo successivo nella descrizione dei sistemi fisici fu fatto da de Lagrange: egli mostrò che il fisico non è vincolato, nella scelta delle coordinate con cui descrive la configurazione di un oggetto, alle coordinate cartesiane dell’oggetto: in realtà, qualsiasi insieme di grandezze o misurazioni da cui si può risalire alle posizioni e alle velocità di un sistema può costituire un sistema di coordinate. Esistono in realtà infiniti insiemi di parametri che possono fungere da coordinate, ed è possibile scegliere quelli più adatti a trattare matematicamente il problema che si ha dinanzi; l’unica cosa che hanno in comune questi insiemi di parametri è il numero: esso è sempre pari ai gradi di libertà del sistema. Questi insiemi di parametri prendono il nome di coordinate lagrangiane. Per chiarire il concetto svilupperemo l’esempio classico di un sistema meccanico costituito da particelle in moto.

Supponiamo di incollare alla parete di un montacarichi un tubo trasparente di gomma, e, mentre il montacarichi sta salendo con velocità costante k, di lasciar cadere nel tubo una pallina.

Matematicamente, abbiamo un sistema bidimensionale formato da una particella puntiforme vincolata a muoversi su una curva di equazione x₂ = x₁² (supponendo che questa equazione descriva la curvatura del tubo di gomma) e che è sottoposta ad un campo gravitazionale uniforme i cui vettori sono paralleli all’asse y e con verso contrario.

Il vincolo risultante dal fatto che la particella si può muovere solo lungo la curva ascendente è esprimibile con la formula:

y = x² + kt

e cioè:

–x² –kt + y = 0

La presenza del vincolo fa sì che le coordinate cartesiane siano in realtà dipendenti l’una dall’altra: il sistema ha quindi non due, ma un grado di libertà.

Piuttosto che attribuire alla particella due coordinate, x e y, un modo più economico di esprimere la sua posizione è quindi quello di rimuovere i parametri dipendenti (cioè che possono essere ricavati da altri parametri) e coordinatizzarla con i soli parametri indipendenti, che prendono il nome di coordinate generali o lagrangiane.

Non esiste un solo modo per scegliere le coordinate lagrangiane, ma piuttosto infiniti. Noi sceglieremo come coordinata lagrangiana il valore di x₁, dal quale si può immediatamente calcolare il valore di x₂.

Usualmente, per distinguere dalle coordinate cartesiane, indicate con x_i, le coordinate lagrangiane vengono indicate con q_i.

Poiché la particella è in movimento, le coordinate lagrangiane, come le coordinate cartesiane, sono funzioni di t, e andrebbero scritte come q_i(t). In quanto tali esse possono essere derivate rispetto al tempo.

Esiste una precisa corrispondenza tra coordinate lagrangiane e coordinate cartesiane. Abbiamo dunque delle equazioni di trasformazioni di coordinate:

x = x(q₁,…,q_n)

y = y(q₁,…,q_n)

Proseguendo nel nostro esempio, essendoci solo la coordinata q₁ scriviamo:

x = x(q₁)

y = y(q₁)

e cioè:

[0708091855] x = q₁

[0708091855] y = q₁² + kt

Il vincolo che abbiamo introdotto è un vincolo dipendente dal tempo, perché le espressioni mostrano che il piano inclinato si trasla in alto con moto uniforme.

Il sistema ha anche delle condizioni iniziali q₁⁰, x⁰, y⁰ che sono utilizzate per integrare le equazioni differenziali che esprimono e condizioni del sistema in un momento di tempo t qualsiasi.

Possiamo ora esprimere il vettore posizione della particella come funzione delle coordinate lagrangiane e del tempo:

x = x(q₁, t)

y = y(q₁, t)

La presenza di t non significa altro che nelle [0708091855] il tempo compare come variabile. Questo indica una doppia dipendenza di y dal tempo: in ogni tempo t il valore di q₁²(t) va modificato di una quantità dipendente direttamente dal tempo, che non è inglobata in q₁.

Niente impedisce di considerare come coordinata lagrangiana il valore dell’espressione x² + kt : in questo caso, terminologicamente, il vincolo non sarebbe dipendente dal tempo.

La particella, sotto l’effetto della forza gravitazionale, è in movimento. Possiamo calcolare il valore della componente verticale v_y della velocità ed esso risulta:

[0708061900]

Essa non è altro che l’applicazione del chain rule o regola di derivazione delle funzione composte:

[0708091906]

dove l’ultimo addendo si riduce chiaramente a ∂y/∂t

Possiamo considerare un esempio semplificato, lineare, che ci permette di interpretare meglio le derivate, in cui il vincolo sia una retta con pendenza +2 che si sposta verso l’alto. Allora si ha:

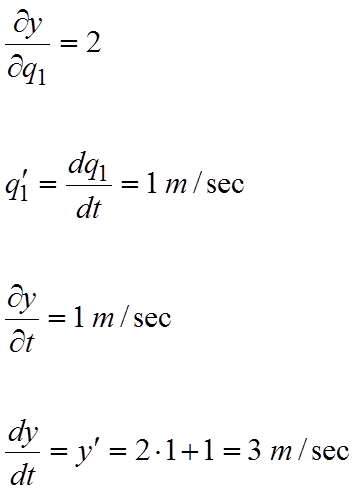
In questa formula le q_i′ sono dette velocità generalizzate.

ipersuperfici e varietà (manifolds)

Generalizzazione del concetto di superficie

back to index

Abbiamo visto che il concetto di piano può essere generalizzato nel concetto di iperpiano, che è un insieme di punti le cui coordinate sono soluzioni di una equazione del tipo:

F(x₁,x₂,…,x_n)

Nello stesso modo si descrive in tre dimensioni una superficie generica; ad esempio l’equazione di una sfera di centro (0,0,0) e raggio 1 (figura 0705181040), è la seguente:

x₁² + x₂² + x₃² = 1

Il luogo dei punti che soddisfa una singola equazione algebrica in cui compaiano tutte le coordinate, cioè un polinomio

F(x,y,z) = 0

di grado n arbitrario in cui compaiano monomi con potenze di x, y, z in grado arbitrario è una superficie algebrica.

Possiamo facilmente generalizzare il concetto in quello di ipersuperficie algebrica: il luogo dei punti che in uno spazio n-dimensionale soddisfa l’equazione:

[0705191645] F(x₁,x₂,…,x_n) = 0

Analogamente, se l’equazione non è algebrica (equazione trascendente), si ottiene la definizione di ipersuperficie trascendente.

All’idea intuitiva di superficie come parte che delimita un corpo, la matematica sostituisce il concetto di un ente geometrico a due dimensioni nel quale ogni punto dipende essenzialmente dal valore di due numeri, detti parametri.

Queste superfici hanno in comune una proprietà tipica delle superfici in tre dimensioni: di dividere lo spazio prossimo ad esse in due parti. Si vede infatti che i punti dello spazio che non appartengono alla superficie si dividono due insiemi: l’insieme dei punti le cui coordinate, sostituite nella [0705191646], danno valore maggiore di zero, e l’insieme dei punti le cui coordinate, sostituite nella [0705191646], danno valore minore di zero.

Per tornare all’esempio della sfera di centro (0,0,0) e raggio 1 la equazione:

x₁² + x₂² + x₃² = 1

può essere scritta in forma implicita:

x₁² + x₂² + x₃² – 1 = 0

Se poniamo il punto di coordinate (1/2,0,0) in tale equazione otteniamo – 3/4, il che mostra che i punti all’interno della sfera hanno coordinate che danno valore negativo e i punti all’esterno positivo.

Una superficie espressa sotto forma di equazione si dice espressa in forma implicita. Un altro modo di esprimerla è quello detto parametrico. All’idea intuitiva di superficie come frontiera di un solido geometrico o contorno di una porzione limitata di spazio, avente solo due dimensioni la matematica sostituisce il concetto di un ente geometrico a due dimensioni nel quale ogni punto dipende essenzialmente da due numeri, detti parametri. Così, una superficie in tre dimensioni sarà definita come l’insieme dei punti le cui coordinate x₁, x₂, x₃ sono quelle espresse da tre equazioni del tipo:

x = f₁(u,v)

y = f₂(u,v)

z = f₃(u,v)

al variare dei due parametri u,v definiti in un adeguato intervallo ( u₁ ≤ u ≤ u₂, v₁ ≤ v ≤ v₂)

Ad esempio, la sfera di cui sopra può essere espressa come:

x = r sen u cos v

y = r sen u sen v

z = r cos u

per 0 ≤ u,v < 2π (vedi figura 0705200810)

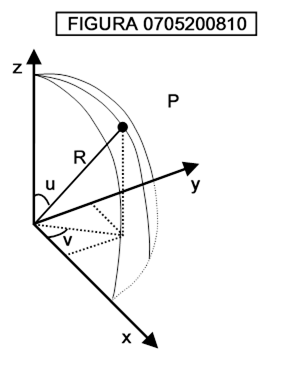
Così vediamo come il concetto di superficie può essere generalizzato in due modi diversi, corrispondenti a due proprietà distinte di una superficie nello spazio tridimensionale:

(A) Una superficie divide lo spazio prossimo ad essa in due parti (forma di equazione implicita)

(B) Una superficie può essere definita da due parametri (forma parametrica)

In spazi con dimensioni superiori a tre questi concetti portano a differenti definizioni di superficie. Abbiamo visto che il concetto (A) porta a quella che viene chiamata “ipersuperficie”. Il concetto (B) porta alla nozione di “manifold bidimensionale”, la cui definizione è data in termini di n equazioni di due variabili (parametri):

x₁ = f₁(u,v)

x₂ = f₂(u,v)

.................

x_n = f_n(u,v)

Le varietà (manifolds)

back to index

Abbiamo visto che in uno spazio 4-dimensionale esiste un sottoinsieme di punti le cui coordinate (p,q,r,s) sono individuate dalla equazione:

(p – r)² + (q – s)² = d²

che rappresenta le posizioni di una sedia. Vedremo più avanti che in uno spazio tridimensioniale in cui le variabili x,y,z rappresentano le quantità vendute di tre diversi tipi di prodotti da parte di una impresa l’iperpiano di equazione ax + by + cz = P rappresenta i punti in cui il profitto è pari a P. Vedremo ancora che gli stati di un sistema periodico sono rappresentati da una linea chiusa nello spazio delle fasi.

Ci rendiamo così conto che all’interno degli iperspazi ci sono set di punti di particolare importanza. Essi costituiscono altrettanti esempi degli oggetti matematici chiamati varietà (inglese manifold).

Il concetto di varietà è uno dei più importanti della matematica moderna. In pratica una varietà è una generalizzazione della nozione di superficie per un numero arbitrario di dimensioni e per spazi più generali di quelli euclidei (ne abbiamo visto diversi esempi).

Quindi i tipi più semplici di varietà sono quelle a una sola dimensione nello spazio euclideo bidimensionale (le curve nel piano, con la retta come caso particolare) e quelle a due dimensioni nello spazio euclideo tridimensionale (le superfici nello spazio, con il piano come caso particolare).

Il concetto di varietà di ordine n in un m-spazio euclideo coincide col concetto di ipersuperficie parametrizzabile con n parametri u₁,u₂,…,u_n che abbiamo esposto più sopra.

Ad un livello più complesso, esistono insiemi di punti come quelli delle posizioni della sedia in un 4-spazio individuati da tre coordinate e non da due (determinando i soli tre valori di p,q,r rimane determinato il valore di s).

Ma esistono varietà più “esotiche”, come l’insieme delle ellissi in R³ con il fuoco in (0,0,0), o, come abbiamo visto, l’insieme delle posizioni di una sedia in uno spazio quadridimensionale o l’insieme delle posizioni di un pendolo nel suo spazio delle fasi bidimensionale o l’insieme di tutti i possibili cerchi in R³.

Limitandoci alle varietà dette aperte contenute in iperspazi di maggiore dimensione (cosiddette varietà immerse o embedded manifolds), che sono più vicine al concetto intuitivo di superficie in uno spazio tridimensionale, si può definire una varietà topologica (il tipo più semplice) di dimensione n come un insieme di punti di un iperspazio a ciascuno dei quali sono assegnate coordinate (x₁,x₂,…,x_n) per mezzo di una serie di mappe interallacciate che “coprono” tutta la varietà. Ogni mappa è una porzione di Rⁿ che ha la caratteristica di essere una esatta “copia” della porzione di varietà rappresentata, non nel senso che conserva distanze o angoli, ma nel senso che conserva la topologia, cioè la posizione reciproca dei punti.

Possiamo renderci conto di questo proiettando una calotta sferica S sulla porzione di piano rappresentata dal disco S’ (figura 0711111512): né le distanze né gli angoli saranno conservati, ma due punti vicini sulla calotta saranno ancora vicini se proiettati sul disco e un punto A separato da un punto B da altri punti sarà ancora separato se proiettato sul disco.

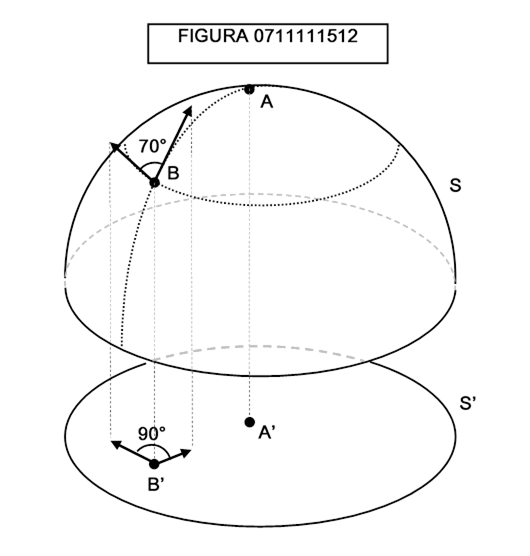
Una simile rappresentazione si dice omeomorfa.

L’insieme delle mappe prende il nome di atlante della varietà. Perché non una sola mappa? Perché per certe varietà non è possibile “proiettare” i punti su un’unica carta in modo bijettivo mantenendo la stessa posizione reciproca. Pensiamo ad esempio ad una sfera: essa non può essere proiettata su alcun piano esterno senza che si abbiano duplicazioni.

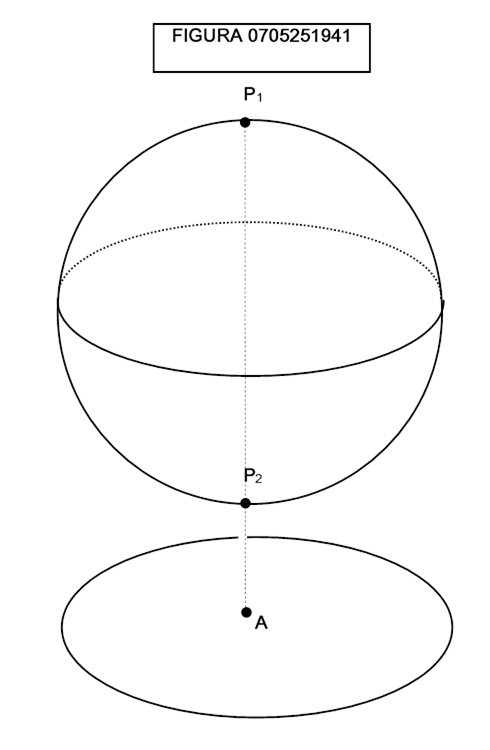
Nella figura 0705251941 la proiezione lungo la linea tratteggiata collega al punto A non uno, ma due punti P₁ e P₂ della sfera, quindi non è bijettiva.

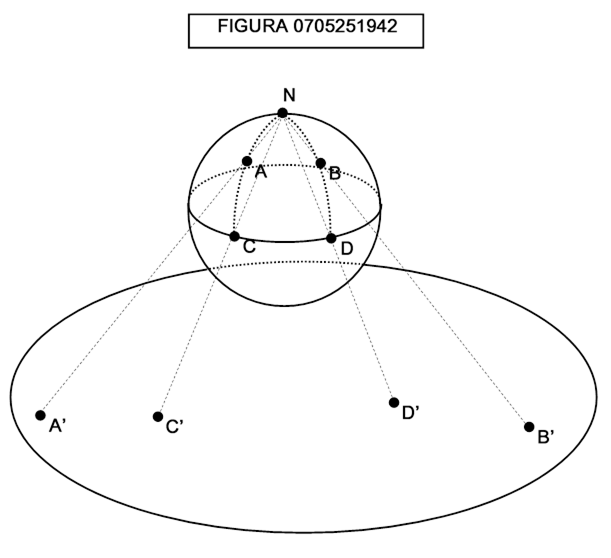
Nella figura 0705251942 la proiezione detta stereografica, per quanto ingegnosa, non riesce a proiettare il punto N, corrispondente al polo nord. Facendo corrispondere questo punto ad un qualsiasi punto di R² non si conserverebbe la sua posizione rispetto agli altri punti. Quindi la proiezione stereografica su un unico piano non è omeomorfa.

Un modo di coordinatizzare la sfera è in realtà quello di proiettare i sei emisferi diversi che possono essere individuati su di essa su altrettanti piani R² (figura 0705251943)

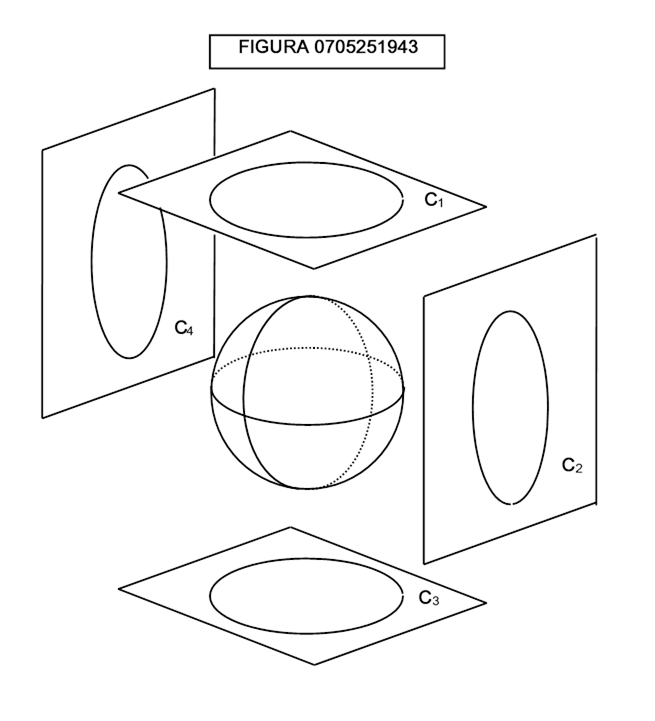
In tal modo si ottiene un atlante composto da 4 carte: C₁, C₂, C₃, C₄.

Le singole carte dell’atlante sono interallacciate: una descrizione completa della varietà deve riportare anche il modo in cui, nelle regioni in cui esse si sovrappongono, le coordinate di una carta si trasformano in quelle dell’altra carta relative al medesimo punto.

Che cosa differenzia le varietà dagli iperspazi in cui sono immerse? Assolutamente nulla: entrambi hanno una dimensione e dei punti – e le varietà normalmente hanno un numero infinito di punti esattamente come gli iperspazi. Entrambi sono dotati di una topologia. Entrambi possono avere una metrica. Anche le varietà possono essere studiate come oggetti a sé stanti, senza riferimento allo spazio che le contiene: tanto è vero che una varietà che può essere immersa in uno spazio tridimensionale può essere immersa altrettanto bene in uno spazio di dimensione superiore.

Non a caso alcuni autori usano i termini manifold, variety, hyperspace come sinonimi.

Le varietà differenziabili

back to index

Varietà come le ipersuperfici sorgono naturalmente in relazione a problemi di analisi matematica e fisica. Lo studio di tali problemi richiede però la possibilità di usare il calcolo differenziale e integrale sviluppato per gli spazi euclidei anche sulle varietà; è ad esempio desiderabile derivare una funzione il cui dominio non sia il familiare spazio R² ma una varietà costituita da una superficie curva; oppure calcolare con passaggi al limite la lunghezza di una linea su una varietà dotata di una metrica non-euclidea.

Il calcolo differenziale tradizionale che il lettore probabilmente conosce meglio, quello delle funzioni reali di una variabile reale (o, come viene indicato nei testi universitari, delle funzioni R → R) o delle funzioni reali di due variabili reali (o funzioni R² → R) è assolutamente inadeguato, ed è stato il compito di diverse generazioni di matematici generalizzarlo ed estenderlo in modo da poterlo applicare alle varietà.

La prima generalizzazione è stata attuata passando da funzioni R → R a funzioni Rⁿ → R^m, dette funzioni a valori vettoriali di variabile vettoriale. Per “vettori” si intendono qui i vettori dati da enople di numeri reali. Una tipica funzione a valori vettoriali di variabile vettoriale è espressa da m funzioni coordinate di n variabili:

y₁ = f₁(x₁,…,x_n)

………………..

y_m = f_m(x₁,…,x_n)

essa porta un generico punto (x₁,…,x_n) ∈ Rⁿ nel punto (y₁,…,y_m) ∈ R^m che costituisce la sua immagine attraverso la funzione f. Centrale nel calcolo multivariato è la nozione di derivata direzionale di tale funzione f in un punto (x₁,…,x_n) del dominio lungo un vettore di coordinate (r₁,…,r_n). Il valore che si ottiene è un vettore di R^m che costituisce il risultato della derivazione vettoriale su Rⁿ.

Il passo successivo consiste di dotare al varietà di carte che la fanno somigliare localmente ad Rⁿ. Se esiste un atlante di carte che copre tutta la varietà (si pensi alla superficie sferica di cui si è detto sopra) e il passaggio da una carta all’altra avviene in modo continuo, cioè è un diffeomorfismo, allora la varietà somiglia localmente ad Rⁿ, cioè i suoi punti hanno coordinate costituite da enople di Rⁿ e quindi le funzioni da una varietà verso un’altra varietà ci appaiono come funzioni multivariate Rⁿ → R^m, che possono essere trattate con i metodi del calcolo multivariato.

Un sistema di coordinate che consente di applicare i metodi del calcolo multivariato anche a superfici curve e in genere a varietà multidimensionali prende il nome di struttura differenziabile. Due varietà che possiedono la stessa struttura differenziabile sono più che omeomorfe, sono diffeomorfe. Un diffeomorfismo è un omeomorfismo infinitamente differenziabile che possiede una inversa infinitamente differenziabile.

Come già visto, ci sono varietà estremamente astratte come “l’insieme delle posizioni di un’asta su un piano o in uno spazio tridimensionale”; “l’insieme delle posizioni delle circonferenze di raggio unitario nello spazio tridimensionale”; “L’insieme delle ellissi nello spazio tridimensionale con uno dei fuochi nel punto di coordinate (0,0,0)”, eccetera.

Il concetto di varietà stimola a sua volta la generalizzazione di ulteriori concetti geometrici. Ad esempio il concetto di linea retta come tragitto più breve tra due punti viene generalizzato in quello di geodetica. Su una superficie sferica le linee più brevi sono i diametri di cerchio massimo, e non esiste una sola linea più breve tra due punti, ma ne esistono infinite. In alcuni particolarissimi casi non ne esiste nessuna.

Le varietà e i tensori

back to index

Uno strumento molto potente per lo studio delle varietà, che permette di svincolarlo dal sistema di coordinate particolare con cui si ha a che fare, è il calcolo tensoriale, sviluppato alla fine dell’Ottocento dai matematici italiani Ricci-Curbastro e Levi-Civita e impiegato da Einstein, insieme alla geometria riemanniana, nella teoria della relatività generale. Esso si basa sul concetto di tensore, che è una generalizzazione del familiare concetto di vettore. Le leggi fisiche o matematiche, espresse in forma tensoriale, acquistano una straordinaria eleganza e semplicità.

la topologia

Le varietà e la topologia

back to index

Le varietà topologiche sono oggetto di studio di quella disciplina matematica che prende il nome di topologia. Della topologia è difficile dire se è più sorprendente la natura rivoluzionaria dei contenuti e l’impatto sulle altre branche della matematica^(0612101659) o il fatto che sia stata scoperta solo dopo 5000 anni di pensiero matematico. Sebbene qualche teorema topologico era noto a studiosi come Leonhard Euler già nel Settecento, l’inizio della disciplina si fa propriamente risalire all’inizio del Novecento.

La topologia studia le proprietà di un insieme di punti invarianti per deformazione continua. Queste proprietà sono chiamati invarianti topologici. Consideriamo ad esempio un foglio quadrato di gomma sottilissima e infinitamente deformabile. Distanze, angoli, aree non si conserveranno quando ad es. lo deformiamo fino ad ottenere una calotta semisferica. Ma la posizione reciproca dei punti si conserva: due punti che erano separati da altri punti prima della deformazione lo saranno ancora dopo la deformazione. Due linee chiuse sulla superficie saranno ancora linee chiuse. Due linee che avevano in comune un punto avranno ancora in comune un punto. E così via.

Il correlativo di questa affermazione è che non si può passare, per deformazione topologica da un insieme di punti che ha determinate caratteristiche topologiche ad un insieme che ha caratteristiche differenti: per quanto si deformi il foglio quadrato, che è una superficie aperta, non si riuscirà ad ottenere una sfera, che è una superficie chiusa, cioè senza “bordi”. Per quanto si deformi una sfera, non si riuscirà a trasformarla in una ciambella o toro, che è una superficie dove esistono linee chiuse che non possono essere deformate con continuità fino ad ottenere un punto: il numero di “buchi” di una ciambella doppia, tripla ecc. è un invariante topologico. Per quanto si deformi il nastro di Moebius non si riuscirà ad ottenere un cilindro, perché un cilindro ha due superfici, mentre il nastro di Moebius ne ha una sola. E così via. Stabilire se una varietà topologica può essere o no trasformata in un’altra costituisce uno dei problemi principali che occupano i topologi. Scherzosamente, la topologia è chiamata anche india-rubber mathematics, cioè matematica del caucciù. Due varietà deformabili l’una nell’altra sono, come vedremo varietà omeomorfe e per il topologo formano un unico oggetto.

Ancora più sorprendente è il comportamento della bottiglia di Klein^(0612100942). La bottiglia di Klein è una superficie chiusa non autointersecantesi che ha una sola faccia. Ma essa non è raffigurabile come tale in uno spazio tridimensionale, perché non è possibile costruire una superficie chiusa ad una sola faccia senza farla passare attraverso se stessa, come si vede dalla figura 0705260710). L’immagine tridimensionale è quindi una pura approssimazione descrittiva di una superficie che può essere rappresentata in modo soddisfacente solo passando ad uno spazio a 4 dimensioni.

La nozione di “posizione reciproca” dei punti è alquanto vaga. Una delle maggiori conquiste della topologia sta nell’aver individuato una serie di concetti che descrivono in modo rigoroso e completo la nozione imprecisa di “posizione reciproca” dei punti di un insieme. Consideriamo ad esempio la forma che assumono tali concetti nella topologia euclidea del piano R², che è quella che viene correntemente insegnata agli studenti e che costituisce la base per l’analisi matematica, il calcolo differenziale e il calcolo integrale.

Consideriamo un insieme S in R². Col termine di intorno di un punto p in R² si definisce l’insieme di punti che distano da p una distanza inferiore ad una distanza data d o un qualsiasi insieme contenente questi punti. Se il concetto di distanza introdotto in R² è euclideo, allora ogni intorno contiene un’area circolare in R²avente un raggio positivo d e centro in p definito intorno circolare di raggio d. L’intorno di un punto p in un insieme è l’intersezione dell’intorno di p e dell’insieme. Si dice insieme aperto un insieme ciascuno dei punti del quale ha un intorno completamente composto da punti dell’insieme. Si parla in tal caso di punti interni. Un intorno aperto è semplicemente un intorno che è un insieme aperto. L’insieme dei punti interni di un insieme costituisce il suo interno. Un punto di S che possiede un intorno formato di punti diversi da punti di S si dice punto isolato di S. Un punto p in ogni intorno del quale cadono punti di S diversi da p si dice punto di accumulazione. Un punto p in ogni intorno del quale cadono sia punti di S (che potrebbero essere anche p) e punti non appartenenti ad S si dice punto di frontiera. Tra i punti di frontiera rientrano evidentemente anche i punti isolati, perché in ogni loro intorno cadono punti appartenenti ad S (loro stessi) e punti non appartenenti ad S. L’insieme dei punti interni e dei punti di frontiera di un insieme rappresenta la chiusura di un insieme. Un insieme che coincide con la propria chiusura si dice insieme chiuso. Un insieme che coincide col proprio interno si dice insieme aperto. Tutto questo può essere visualizzato con una figura (figura 0705260702).

Una funzione da un insieme S ad un insieme T collega ad ogni punto p di S uno ed un solo punto di T f(p) chiamato immagine del punto p. Una funzione si dice bijettiva se ad ogni punto di S corrisponde un solo punto di T e ogni punto di T ha una sola controimmagine in S. Nel caso di bijezione, la funzione che porta ogni punto di T nella sua unica controimmagine in S è detta funzione inversa della funzione f. Dato un insieme V di T l’insieme U dei punti di S le cui immagini sono in V costituisce la controimmagine del sottoinsieme V di T. Una funzione da S a T si definisce funzione continua se la controimmagine di un insieme aperto di T è ancora un insieme aperto di S. Una funzione bijettiva e continua, la cui inversa sia ancora continua si dice omeomorfismo. Il concetto di omeomorfismo è estremamante importante in topologia: due insiemi di punti omeomorfi hanno la stessa posizione reciproca e possono essere deformati con continuità l’uno nell’altro.

Espressa nel linguaggio della topologia, la definizione di varietà suonerebbe all’incirca così: una varietà topologica di ordine n è un insieme ogni punto del quale ha un intorno aperto omeomorfo ad un intorno aperto di Rⁿ.

Giochi topologici

back to index

Osserviamo la figura 0705210803, dove sono mostrate delle superfici cave di sottilissima gomma che può essere deformata o ristretta a piacimento, ma non tagliata. Siamo in grado di manipolare l’oggetto a sinistra per ottenere quello di destra?

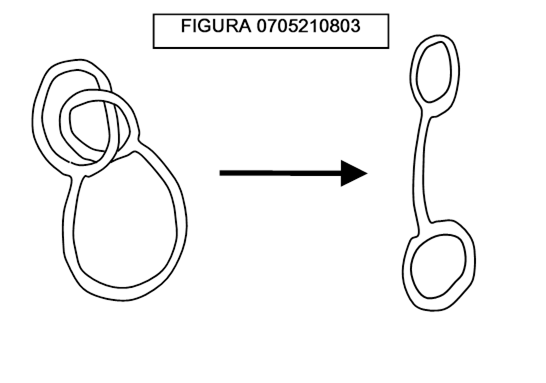
La soluzione è mostrata qui sotto.

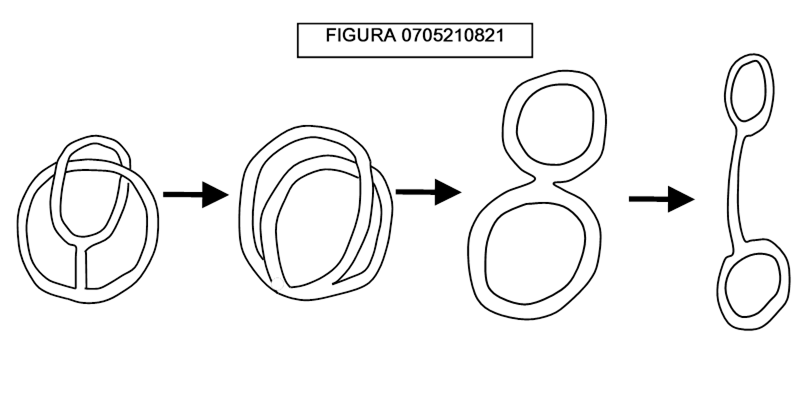
Osserviamo la figura 0705210840: siamo in grado di dire dalla deformazione di quale degli oggetti posti a sinistra si ottiene il bicchiere a destra?

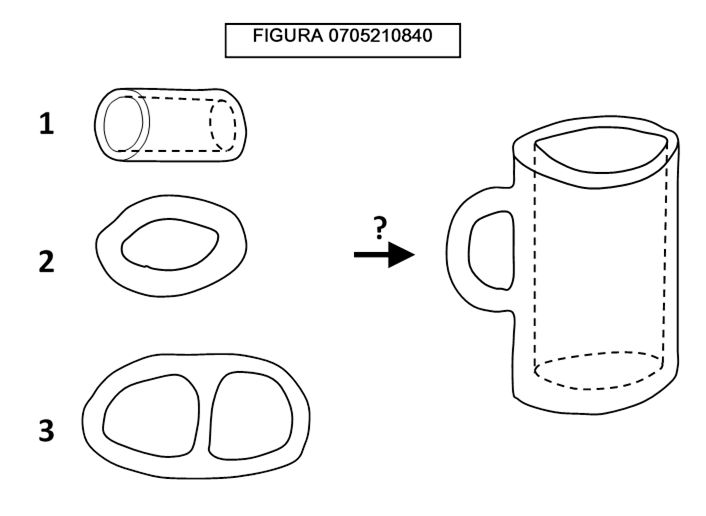
Osservate la figura 0705210905: essa raffigura la “bottiglia di Klein”, che ha la caratteristica di essere “una superficie chiusa non autointersecantesi con una sola faccia”. E’ possibile rappresentare tridimensionalmente questa superficie? La rappresentazione della figura 0705210905 risponde esattamente alla definizione? Se no, qual è il numero minimo di dimensioni in cui una bottiglia di Klein può essere esattamente disegnata?

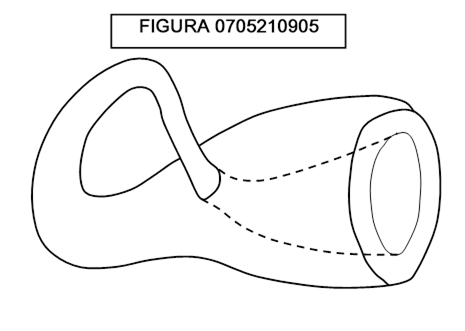
Risposta: la bottiglia di Klein non può essere disegnata esattamente in tre dimensioni perché in ogni caso si autointerseca. Ma in quattro dimensioni essa può penetrare in sé stessa senza intersecarsi, perché in tal caso è possibile spostare i punti della intersezione “un po’ più in là” nella quarta dimensione, in modo che non intersechino la superficie.

Usi degli iperspazi: il problema di re Oscar di Svezia

back to index

Un esempio di uso degli iperspazi è quello che ne fece il matematico Henri-Jules Poincaré^(0612081850). per risolvere un quesito scientifico posto dal re Oscar di Svezia, che mise in palio un premio per la soluzione.

Alla fine dell’Ottocento la scienza astronomica era molto progredita, ma non si era ancora riusciti a dare risposta alla domanda: il sistema solare è un sistema stabile? E cioè: i pianeti continueranno nel loro moto oppure giungerà un momento in cui si allontaneranno l’uno dall’altro nello spazio, collideranno fra di loro o altereranno le loro orbite e la loro distanza dal Sole?

Per quanto possa sembrare sorprendente, la formulazione matematica rigorosa di questa domanda è estremamente difficile, e richiese lo sforzo di una delle menti più notevoli del diciannovesimo secolo.

Tentando di dare una soluzione, Poincaré si rese conto che la posizione e direzione di moto di n corpi celesti in un dato istante t potevano essere descritte come punti di un tipo di spazio chiamato spazio delle fasi, dotato di 2 ⋅ n ⋅ 3 dimensioni in cui le prime 3 ⋅ n coordinate descrivono la posizione di n corpi nello spazio, mentre le rimanenti 3 ⋅ n coordinate esprimono la loro quantità di moto m ⋅ v, che, essendo v un vettore, richiedono parimenti 3 coordinate.

Mentre il sistema si evolve nel tempo, il punto si muove descrivendo una curva. Poincaré ridusse così una successione di stati del sistema a una linea nello spazio delle fasi.

Perché i corpi celesti tornino periodicamente a percorrere le stesse orbite, questa curva deve chiudersi; se osserviamo il percorso tracciato in figura 0705251332, occorre che il percorso sia quello A, che passi di nuovo per il punto iniziale O, e non quello B o C.

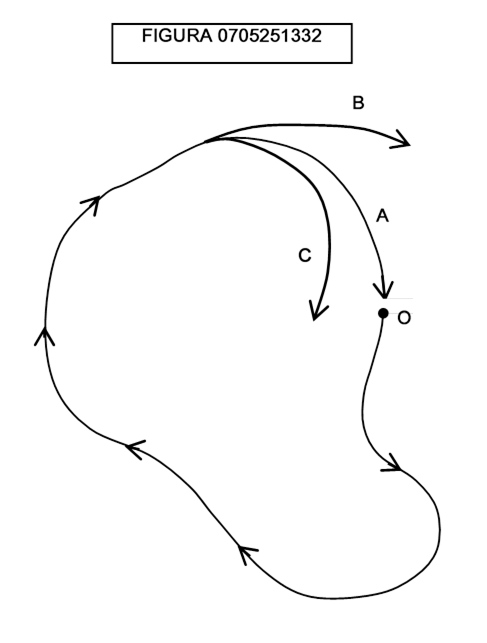
Quand’è che una curva si chiude? Si noti che la domanda non riguarda la forma o la grandezza o la posizione della curva chiusa; si tratta in altre parole di un problema topologico.

L’idea di Poincaré è semplice ed elegante: la curva si chiude se, data una porzione di piano che incorpori uno e un solo punto della curva nel tempo t₀, esista un tempo t₁ in cui il sistema occupi di nuovo lo stesso punto. Questa porzione di piano si chiama sezione di Poincaré. Una volta ripassato per lo stesso punto il sistema deve ripassare per tutti i punti che ha percorso fino a quell’istante, perché abbiamo incorporato nelle coordinate anche le velocità, e non solamente le posizioni. Il fatto notevole è che possiamo posizionare la sezione di Poincaré in un qualsiasi punto della curva: il fatto che si abbia il passaggio nel medesimo punto anche in una sola sezione, implica che la curva che descrive il moto del sistema sia chiusa (figura 0705251341).

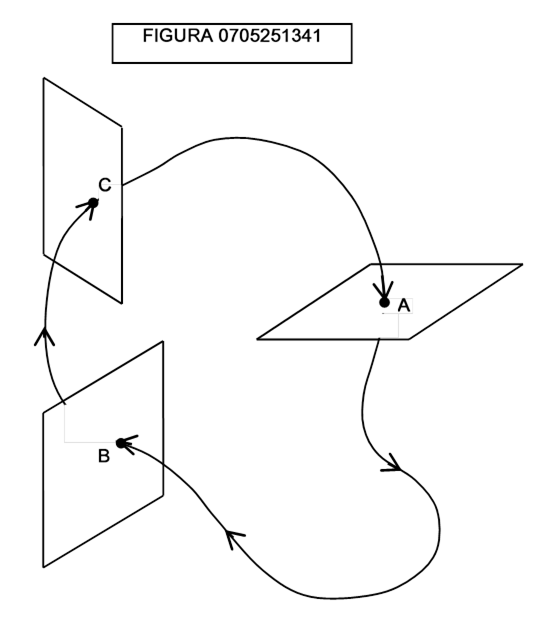
Nella realtà il problema è praticamente insolubile perché l’iperspazio deve comprendere la posizione e quantità di moto di ciascun singolo granello di polvere cosmica: in caso contrario esso sarà un modello incompleto e le previsioni fatte sulla sua base non saranno attendibili. Per questo gli iperspazi che descrivono fenomeni fisici o sociali hanno un numero incredibilmente alto di dimensioni.

Con gli stessi strumenti di dinamica topologica con cui si studia il moto di un sistema fisico come il sistema solare, si può studiare il funzionamento dei sistemi economici per stabilire se determinati fenomeni (es. crisi economiche ed espansioni economiche) hanno un andamento ciclico o no.

gli spazi curvi

La distanza nei manifold e negli iperspazi

back to index

Una caratteristica delle varietà topologiche che può apparire “aliena” e lontana dal senso comune è che molte di esse non posseggono distanze tra i punti e che comunque il concetto di distanza non è essenziale per la loro esistenza.

Noi siamo abituati a spazi in cui sono misurabili distanze. In linguaggio matematico rigoroso, in tali spazi è definita una metrica, cioè una funzione d(p,q) che a due punti qualsiasi p,q assegna un valore chiamato distanza e che possiede le seguenti caratteristiche:

▸ d(p , q) ≥ 0

▸ d(p , q) = 0 ⇒ p = q

▸ d(p , q) = d(q , p)

▸ d(p , r) ≤ d(p , q) + d(q , r)

In altre parole, la distanza può essere qualsiasi cosa, purché abbia tre caratteristiche: a) la distanza di un punto da se stesso è zero; b) la distanza tra due punti è sempre positiva; c) la distanza tra il punto p e il punto q è eguale alla distanza tra il punto q e il punto p; d) la somma della distanza tra p e q e della distanza tra q ed r deve essere non superiore alla distanza tra p ed r.

La metrologia, ad esempio, definisce la distanza di un metro come quella tra due tacche sul metro campione di Parigi, in corrispondenza del punto di partenza e del punto di arrivo di un raggio di luce che ha viaggiato nel vuoto, rasente alla superficie, per il tempo di un trecentomillesimo di secondo, cioè per il tempo che impiega la luce emessa da un atomo di cesio cui sia stata fornita una ben determinata energia addizionale ad oscillare 9.192.631.770 volte nel vuoto.

Possiamo pensare di misurare le distanze disponendo di una fibra ottica monodimensionale (nei libri di fantascienza appaiono fibre monomolecolari, che ne sono un buon sostituto) e perfettamente trasparente, di disporla lungo la superficie in modo che segua la via più breve tra due punti, sincronizzare gli orologi e poi segnare il tempo di partenza e quello di arrivo (Einstein avrebbe qualcosa da ridire). Questo ci permette di calcolare la distanza su superfici curve.

Le distanze che possono essere definite sono le più varie; la metrica euclidea, in cui la distanza viene calcolata, come si è visto, con il teorema di Pitagora, è solo un caso particolare di una metrica più generale, detta metrica riemanniana, che viene definita punto per punto, in modo che, per esprimerci in termini intuitivi, le distanze in un intorno infinitamente piccolo del punto sono date dalla formula generale:

[0705280554] ds² = g_1…1 ⋅ dx₁⋅ dx₁ ⋅ … ⋅ dx₁ + g_1…2 ⋅ dx₁⋅ dx₁ ⋅ … ⋅ dx₂ + … + g_n…n ⋅ dx_n⋅ dx_n ⋅ … ⋅ dx_n

Su una superficie bidimensionale come la calotta sferica di figura 0705262021 la formula diviene:

[0705280555] ds² = g₁₁ ⋅ dx₁ ⋅ dx₁ + g₁₂ ⋅ dx₁ ⋅ dx₂ + g₂₁ ⋅ dx₂ ⋅ dx₁ + g₂₂ ⋅ dx₂ ⋅ dx₂

dove le quantità g_j…k sono le componenti del cosiddetto tensore metrico.

I valori dx₁ e dx₂ indicano uno spostamento infinitesimo in direzione x₁ e uno spostamento infinitesimo in direzione x₂. Il simbolo dx₁ e dx₂ anziché ∆x₁ e ∆x₂ indicano, nel linguaggio tradizionale dell’analisi il passaggio ai differenziali, cioè in sostanza a spostamenti infinitesimi. Osserviamo ora la figura 0705262021;

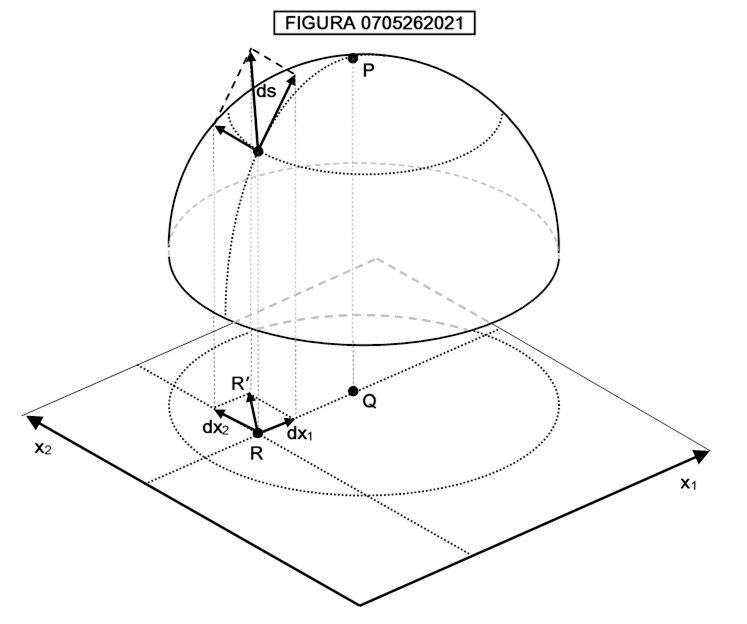
In essa è mostrata una varietà costituita da una superficie a forma di calotta semisferica nello spazio tridimensionale, coordinatizzata mediante proiezione che assegna ad ogni punto della calotta la coordinata del corrispondente punto del piano x₁x₂, detto piano dei parametri . Un tale modo di assegnare le coordinate per proiezione viene detto parametrizzazione di Monge.

Ad esempio, il punto P alla sommità della sfera ha le coordinate assegnate al punto Q nel piano sottostante. I due spostamenti nel piano, componendosi secondo la nota regola del parallelogramma, danno uno spostamento da R ad R′ cui corrisponde, sulla calotta, uno spostamento ds, il cui valore viene appunto calcolato secondo la formula di distanza di Riemann. Il vettore che va da R ad R′ viene detto vettore spostamento (displacement vector). La formula che lega dx₁, dx₂ e ds nel caso di calotta sferica viene ricavata, a titolo di esemplificazione, nel paragrafo successivo a questo. il lettore potrebbe saltare la dimostrazione e leggere la formula [0704230935], che ancora una volta è espressa nella forma [0705280554].

La distanza euclidea nello spazio a tre dimensioni si misura secondo la formula particolare:

ds² = 1 ⋅ dx₁⋅ dx₁ + 1 ⋅ dx₂⋅ dx₂ +1 ⋅ dx₃⋅ dx₃

dove il vettore (dx₁ dx₂, dx₃) rappresenta uno spostamento infinitesimo dal punto p.

Le varietà caratterizzate dalla metrica riemanniana si dicono varietà di Riemann, e sono particolarmente importanti per la teoria generale della relatività.

Proprietà di forma, metriche, topologiche di una superficie

back to index

Per poter capire meglio le proprietà topologiche di una superficie, sviluppiamo le seguenti considerazioni, che richiedono concetti di geometria differenziale, ma che possono essere comprese nelle linee generali anche da chi non possiede le basi di questa disciplina.

Consideriamo una scodella che rigiriamo tra le nostre mani. L’oggetto matematico che modellizza la sua faccia esterna è una superficie curva che subisce traslazioni e rotazioni in un sistema di riferimento tridimensionale.

Ad ogni mutamento cambia l’equazione che descrive la superficie in forma implicita (come dicono i matematici) cioè del tipo

f(x,y,z) = 0

Per peggiorare le cose, scegliendo un altro sistema di coordinate (per es. spostando l’origine degli assi cartesiani o ruotandone la terna) l’equazione cambia ulteriormente.

L’equazione non è quindi lo strumento adatto – o quantomeno immediato – per dar forma matematica alla nostra intuizione che “vede” uno stesso oggetto costituito da una superficie immersa in uno spazio tridimensionale.

E’ possibile stabilire le regole con cui l’equazione cambia: date due equazioni, f(x,y,z) = 0 e g(x,y,z) = 0 esse rappresentano la stessa superficie se con un cambiamento di coordinate si può trasformare l’una nell’altra.

Ma cos’è che rimane matematicamente invariante in questi cambiamenti?

Il problema di isolare i caratteri necessari e sufficienti ad individuare una superficie senza riguardo alla sua posizione nello spazio fu risolto solo a metà dell’Ottocento, con la scoperta della seconda forma fondamentale di una superficie, ad opera di Gauss e dei suoi successori.

Mentre la metrica della superficie viene determinata dalla conoscenza, punto per punto, dei coefficienti E,F,G della espressione (detta prima forma fondamentale):

E ⋅ dx₁² + 2F ⋅ dx₁ ⋅ dx₂ + G ⋅ dx₂²

che fornisce la lunghezza, della derivata direzionale nel punto considerato secondo il vettore (dx₁,dx₂) dello spazio dei parametri, per la determinazione anche della forma indipendentemente dalla posizione è necessario conoscere i coefficienti della seconda forma fondamentale , che fornisce la componente della variazione del vettore normale alla superficie nella direzione della derivata direzionale secondo il vettore (dx₁,dx₂):

L ⋅ dx₁² + 2M ⋅ dx₁ ⋅ dx₂ + N ⋅ dx₂²

Qui non si vuole entrare nel dettaglio di tale teoria, ma solo evidenziare due dei risultati sorprendenti degli studi di Gauss e dei successori: 1) Le caratteristiche di una superficie coordinatizzata possono essere descritte intrinsecamente, senza riferimento ad uno spazio in cui essa è immersa; 2) una metrica non è sufficiente a fissare la forma della superficie.

Senza forse accorgersene gli studiosi avevano formulato la matematica che permetteva di descrivere le proprietà invarianti di un foglio di carta quadrettato arrotolato, appallottolato, utilizzato per fare origami.

Sembra proprio che l’unica cosa che contraddistingua una superficie inestensibile ma ripiegabile siano le qualità metriche (chiamate qualità intrinseche della superficie) determinate dalla sola prima forma fondamentale.

Le qualità metriche, che sono indipendenti dal modo in cui la superficie è immersa nello spazio, fanno parte del gruppo delle proprietà intrinseche della superficie. Le proprietà intrinseche di una superficie, approssimativamente parlando, sono quelle che possono essere misurate o scoperte da un essere bidimensionale che vive interamente sulla superficie.

Si era in tal modo fatto un passo avanti decisivo verso la individuazione di gruppi di proprietà indipendenti di una superficie.

Se togliamo anche le proprietà metriche e lasciamo solo le proprietà di posizione reciproca otteniamo uno spazio topologico, che non è più un foglio di carta, ma un foglio di gomma sottile.

Così, quando ad una varietà di ordine 2 come una superficie in R³ o in dimensioni più alte si aggiunge una metrica la trasformiamo da foglio di gomma a fazzoletto di seta: una estensione indeformabile ma infinitamente ripiegabile. Una delle più grandi sorprese dei matematici fu la scoperta che fissare una distanza tra i punti di una superficie non ne determina in modo unico la forma. Un sottilissimo fazzoletto di seta ha una distanza fissa due suoi punti qualsiasi, e quindi non è deformabile come un foglio di gomma, ma non ha una forma definita: può stare nel nostro taschino o essere dispiegato sulle nostre ginocchia.

Gli spazi curvi bidimensionali

back to index

Quanto detto sul concetto di distanza vale anche per gli iperspazi che contengono le varietà. Pochi anni dopo la scoperta delle geometrie non euclidee ad opera di Bolyai e Lobacevskji, Bernhard Riemann^(0612081856) si rese conto che ogni geometria dipende dalla metrica che si definisce su una superficie.

Immaginiamo una “formica puntiforme”, cioè un animaletto costituito da un unico punto geometrico. Se la formica è costretta a vivere entro una linea curva senza poterne uscire allora diciamo che vive in uno spazio monodimensionale curvo.

Una formica che vive sulla superficie di una sfera o di un iperboloide o di un’altra superficie curva vive in uno spazio bidimensionale curvo. Se la formica vive in un piano essa vive in uno spazio bidimensionale euclideo.

Come può la formica rendersi conto se il suo spazio è uno spazio euclideo o uno spazio curvo? Un metodo sarebbe quello di andare in orbita su una navetta spaziale, guardare giù e constatare che la superficie è curva. Ma il nostro animaletto è bidimensionale, cioè non può muoversi in tre dimensioni. Allora dovrebbe utilizzare un sistema alernativo, consistente nel piantare due lunghissimi filari paralleli di alberi, col seguente metodo, che si può immaginare ad es. applicato ad una superficie sferica (figura 0705261732).

Tiriamo ben bene una cordicella da un punto A ad un punto B, e a metà piantiamo il primo albero H. Poi tendiamo due cordiicelle di eguale lunghezza da A e B e piantiamo l’albero D dove esse si incontrano. Poi raddoppiamo la lunghezza delle cordicelle e, nel punto del loro incontro, piantiamo l’albero G. Proseguiamo così indefinitamente. Con la stessa operazione piantiamo gli alberi I, E, F… del filare di destra.

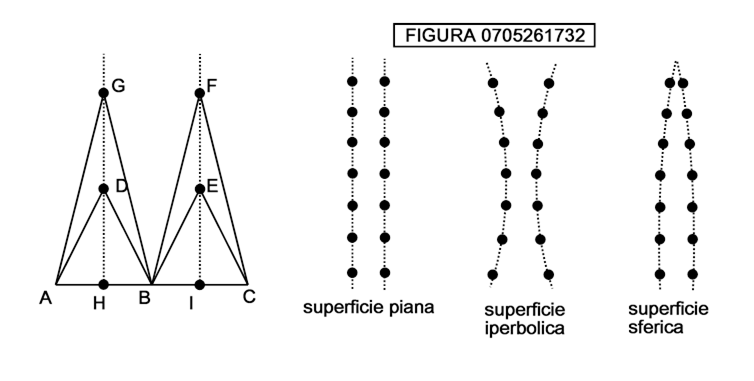
Se, proseguendo all’infinito la piantagione i due filari si avvicinano siamo in uno spazio curvo sferico; altrimenti in uno spazio curvo iperbolico. Se gli alberi non giungono mai a toccarsi allora siamo in uno spazio euclideo (superficie piana). Nella figura 0705261733 sono mostrate, in alto, parti ingrandite rispettivamente della sfera e dell’iperboloide a una falda, che è una superficie quadrica, cioè rappresentata da una equazione polinomiale di secondo grado in x, y, z del tipo:

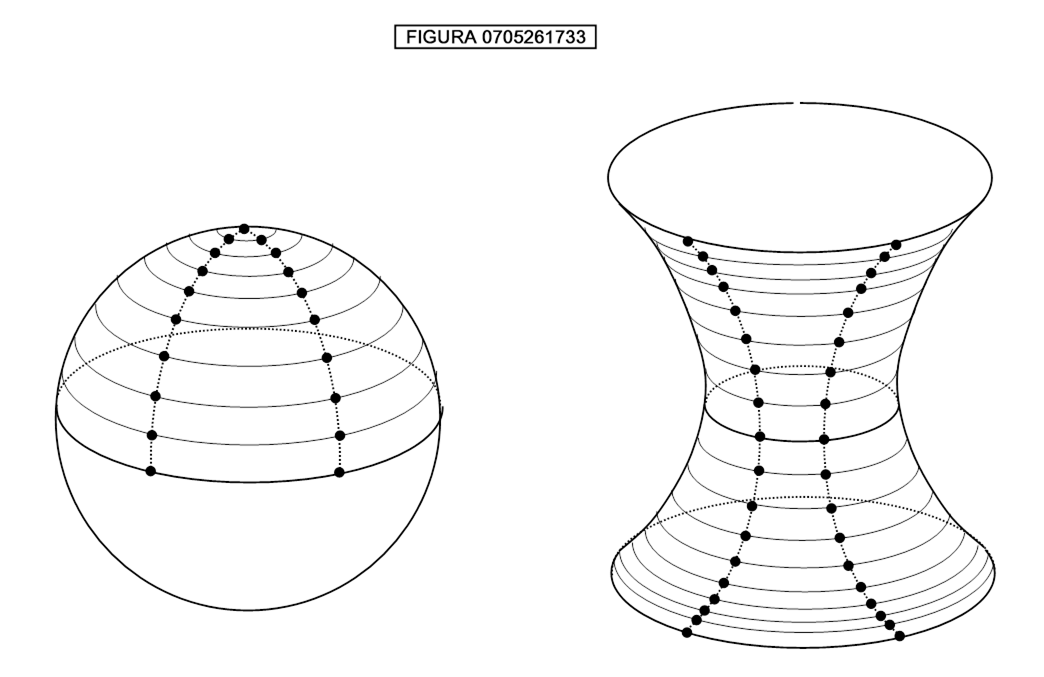
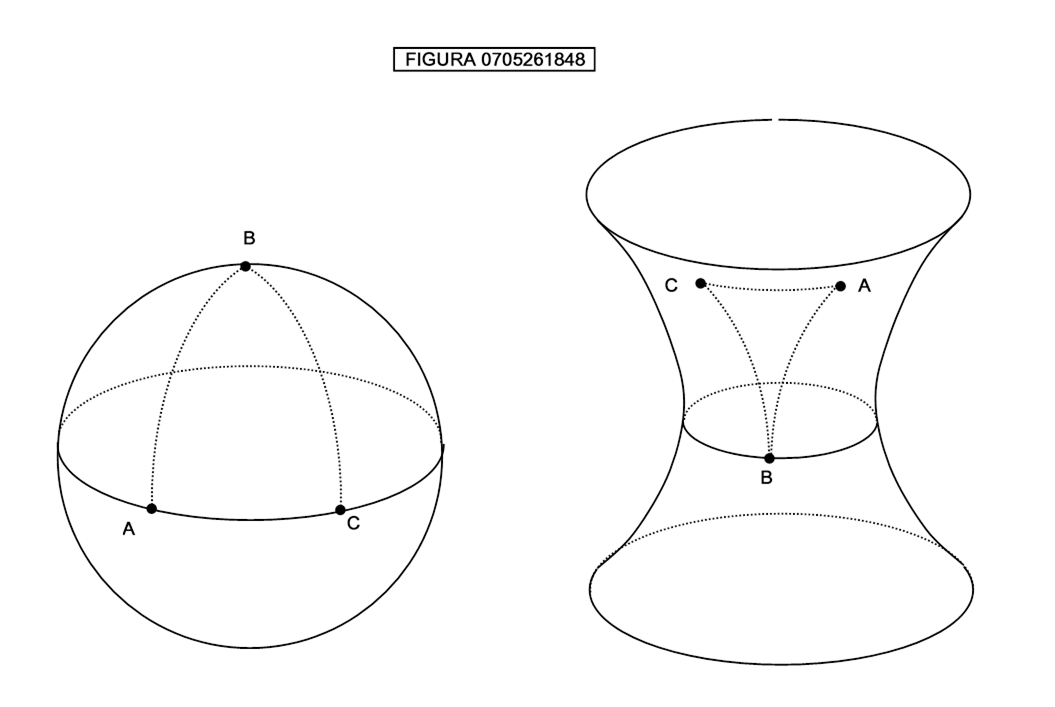
Un altro modo per rendersi conto se si vive su un piano o no è quello di misurare l’area di un triangolo disegnato sulla superficie: se l’area è inferiore a quella ottenuta con le formule di geometria euclidea allora la superficie è iperbolica; se l’area è superiore allora la superficie è sferica (figura 0705261848).

Un altro modo di rendersi conto se la Terra è curva è il seguente: Partite dal Polo Nord e viaggiate verso sud per circa 10000 chilometri, dopo aver preso nota della direzione iniziale. Quindi virate verso sinistra ad angolo retto e percorrete la medesima distanza. Virate ancora verso sinistra e percorrete la medesima distanza. Poiché 10000 chilometri è all’incirca la distanza del polo dall’equatore il vostro viaggio vi avrà portati dal Polo Nord all’equatore, quindi lungo l’equatore per un suo quarto e infine nuovamente al polo Nord. Inoltre, la direzione lungo la quale avete fatto ritorno forma un angolo retto con quella di partenza. Ne segue che sulla superficie della Terra esiste un triangolo equilatero con tutti gli angoli retti. Su una superficie piana, però, gli angoli di un triangolo equilatero devono essere di 60 gradi – sono uguali e la loro somma è 180 gradi –, quindi la superficie della Terra non è piana.

Sempre in riferimento all’esempio precedente, si può notare che il teorema di Pitagora, applicato al triangolo ABC, con il lato BC interpretato come ipotenusa e i lati AB e AC interpretati come cateti non fornisce i valori corretti. Secondo tale teorema la distanza BC sarebbe infatti:

mentre, come abbiamo visto, il valore esatto è 10.000.

Mentre il triangolo ABC sulla sfera a sinistra è detto triangolo sferico, il triangolo ABC sull’iperboloide a destra è detto triangolo iperbolico. La caratteristica di un triangolo iperbolico è di avere la somma degli angoli interni inferiore a 180°

Gli spazi curvi tridimensionali

back to index

L’idea-base di spazio curvo è in realtà molto semplice: in uno spazio curvo non valgono gli assiomi della geometria euclidea. Come i fisici moderni fanno notare, niente assicura che lo spazio in cui viviamo soddisfi gli assiomi di Euclide, e sia cioè uno spazio euclideo. Se non lo facesse sarebbe uno spazio curvo.

Uno dei più grandi matematici tedeschi dell’Ottocento, Gauss, misurò un triangolo con i vertici coincidenti con le cime di monti distanti alcune centinaia di chilometri, per stabilire (si dice) se la la somma degli angoli interni fosse proprio di 180°, come postulato da Euclide.

Nello spazio curvo, non vale in particolare la formula euclidea (pitagorica) della distanza. Questo richiede però alcune precisazioni. La formula euclidea vale solo per un sistema di coordinate cartesiano ortogonale. Lo spazio euclideo, coordinatizzato in coordinate polari cilindriche o sferiche (innumerevoli altri sistemi di coordinate sono parimenti possibili) non possiede una formula di distanza euclidea (questo è stato visto più sopra). Inoltre, per intorni infinitesimi è sempre possibile trovare, anche in uno spazio curvo, un sistema di coordinate tali che la formula di distanza sia quella euclidea (si pensi al punto apicale di una parametrizzazione di Monge di una calotta sferica).

I coefficienti g_jk nella formula:

ds² = g₁₁dx₁dx₁ + g₁₂dx₁dx₂ + … + g_nndx_ndx_n

costituiscono gli n² valori di un oggetto matematico chiamato “tensore metrico”. Dire che la formula di distanza si modifica a seconda del sistema di coordinate vuol dire che i valori del tensore si trasformano secondo una legge legata alle equazioni di cambiamento di coordinate. Questa legge di variazione è detta covarianza.

In gergo matematico possiamo dire che il tensore metrico è unico come la distanza che esprime (la distanza è invariante per trasformazione di coordinate) ma i suoi valori variano in ciascun sistema. Il fatto che il tensore metrico vada pensato come unico non toglie che sia utile disporre di un invariante numerico cioè di un tensore i cui n² valori in un punto non varino al variare delle coordinate e varino da punto a punto solo se la curvatura cambia.

Un tale tensore avrebbe diversi vantaggi rispetto al tensore metrico: ci consentirebbe di stabilire se lo spazio è “flat”, cioè riducibile a coordinate euclidee, semplicemente mediante il confronto con il valore invariante del tensore di curvatura dello spazio euclideo (tale valore è zero), invece di lasciarci nel dubbio, come fa il tensore metrico, che un dato sistema di coordinate possa essere cambiato in un sistema euclideo; inoltre ci direbbe se il sistema ha o no una curvatura costante, cosa che non può essere ricavata dall’esame del tensore metrico, perché i coefficienti g_jk dell’elemento di distanza di uno spazio a curvatura costante, in molti sistemi di coordinate, variano da punto a punto (ad esempio l’elemento di distanza di una calotta sferica, nei sistemi di coordinate diversi da quello latitudine-longitudine varia da punto a punto).

Il tensore di curvatura non è altro che la generalizzazione di una misura della curvatura delle superfici introdotta da Gauss. Egli scoprì una indicatrice, chiamata curvatura gaussiana che, se zero in ogni punto della superficie, rivela una superficie piana, sia pure “arrotolata” in vario modo.

Senza un tensore di curvatura possiamo procedere fino ad un certo punto in modo intuitivo o basandoci sul tensore metrico. Per uno spazio curvo tridimensionale sferico è ancora possibile dimostrare intuitivamente (come faremo) che la distanza tra due punti non è mai euclidea: la difficoltà consiste nel fatto che la non-pitagoricità di un sistema di coordinate non prova necessariamente che non ve ne siano altri che conducano ad una formula pitagorica.

Ma per spazi sferici di dimensione 4 o superiore, o per spazi di curvatura costante non-sferici o addirittura per spazi di curvatura non costante né la curvatura gaussiana né i ragionamenti intuitivi riescono a condurre alla dimostrazione conclusiva che non esiste un sistema cartesiano di coordinate. Necessita il tensore di curvatura.

Purtroppo, la determinazione di tale invariante è alquanto complessa matematicamente. Ad esempio, la curvatura, per lo spazio tridimensionale, è data da sei valori, perché uno spazio tridimensionale può essere curvato in molte direzioni, per ciascuna delle quali può esistere una curvatura diversa.

Una volta posseduto il tensore di curvatura, si può calcolarlo in riferimento allo spaziotempo incurvato dalla gravità e verificare tramite esso che effettivamente non esiste alcuna trasformazione di coordinate che introduca dovunque la distanza euclidea, e quindi concluderne che tutti gli spazi, in presenza della gravità, sono curvi.

Una volta mostrato che il cronotopo è incurvato dalla gravità, possiamo, per semplificare, supporre che esso abbia una curvatura sferica, cioè sia una ipersfera a 4 dimensioni in uno spazio pentadimensionale, come effettivamente si suppone che sia per l’universo su larghissima scala.

Lo spazio fisico non è altro che una “fetta” di cronotopo ottenuta tenendo fermo un istante di tempo t. Si vede facilmente che quel che ne risulta è una ipersfera a tre dimensioni. Come dice Tim Gowers, potremmo scoprire di vivere in realtà non nello spazio di Euclide, ma sulla superficie di una ipersfera a tre dimensioni (una ipersfera a tre dimensioni o S₃ non è una sfera dello spazio tridimensionale parametrizzata con due parametri, bensì una sfera dello spazio tetradimensionale coordinatizzata con tre parametri).

Lo spazio incurvato dalla gravità: la relatività generale di Einstein

back to index

Un noto matematico ha scritto che esiste una seria possibilità che l’universo in cui viviamo sia la superficie tridimensionale di una sfera a quattro dimensioni (anche se non è escluso che lo spazio su grande scala non sia curvo, o che la curvatura sia, anziché positiva, come in questo caso, negativa).

Quello che il matematico in questione si è scordato di precisare (per amore di una malintesa volgarizzazione) è che, in termini matematici rigorosi, la frase suonerebbe così: “esiste una seria possibilità che l’universo in cui viviamo sia una sezione spaziale di un cronotopo costituito da una sfera tetradimensionale in uno spazio pentadimensionale dotato di una metrica flat semiriemanniana di signatura (-1,+1,+1,+1)”. Si tratta di un modello abbastanza semplice di spaziotempo denominato Spazio di de Sitter.

Tralasciando i concetti più avanzati, se il lettore si è sufficientemente familiarizzato con la nozione di cronotopo o spaziotempo della relatività ristretta, egli è pronto ad affrontare un breve cenno di relatività generale.

La intuizione che consentì ad Einstein di incorporare nel suo modello di spazio gli effetti della gravità, e che egli chiamò “la più felice della mia vita”, è la seguente. Immaginiamo di essere in un ascensore, senza contatti con l’esterno, in modo che non possiamo renderci conto se siamo in prossimità o meno di un corpo che genera un campo gravitazionale. Se, lontano da qualsiasi pianeta, l’ascensore viene fatto accelerare uniformemente in direzione normale al lato su cui sono poggiati i nostri piedi (che chiameremo “pavimento”) noi sperimentiamo una forza gravitazionale diretta verso il pavimento; ma lo stesso avviene se l’ascensore, fermo, è posto in prossimità di un pianeta, con il pavimento rivolto verso la superficie del pianeta. Per noi che siamo chiusi nell’ascensore è del tutto impossibile stabilire se la forza attrattiva sia dovuta alla presenza di un campo gravitazionale o ad una accelerazione impressa al sistema.

Supponiamo ora che, mentre l’ascensore viene accelerato, un raggio di luce entri da un forellino posto nella parete alla nostra destra, e colpisca la parete alla nostra sinistra. L’osservatore nell’ascensore noterà che il raggio ha una traiettoria curva. Poiché abbiamo postulato che non si ha modo di distinguere gli effetti di un campo gravitazionale da quelli di una accelerazione del sistema, dobbiamo concludere che un campo gravitazionale ha, sul raggio di luce, lo stesso effetto.

Per poter determinare gli effetti della gravità sul cronotopo, occorre un altro esperimento. Supponiamo che, in un razzo sottoposto ad una forte accelerazione, due sperimentatori, Bill e George, uno presso la punta del razzo, e un altro presso la coda (figura 0711111829). Ad ogni secondo segnato dall’orologio situato nella punta del razzo, bill invia un segnale luminoso a George, che determina l’intervallo tra i segnali in base all’orologio posto nella coda del razzo.

Mentre Bill afferma che gli intervalli dell’orologio sono di un secondo, George osserva che essi sono inferiori ad un secondo, perché l’accelerazione del razzo spinge George in direzione del segnale, facendo sì che esso sia captato meno di un secondo dopo il precedente. Il principio di equivalenza tra accelerazione e campo gravitazionale implica quindi che un campo gravitazionale faccia andare più veloci gli orologi posti in prossimità della sorgente del campo, e cioè posti in un punto in cui il potenziale gravitazionale è minore.

Cerchiamo ora di dare una espressione matematica precisa a questi rilievi. Per semplificare l’analisi supponiamo che il le formule valide per il nostro caso siano quelle newtoniane, senza alcun effetto dovuto alla relatività speciale.

In questo modo possiamo considerare l’esistenza di un unico tempo per i due orologi, e non dobbiamo fare i conti con l’effetto relativistico della contrazione delle lunghezze nel verso del moto.

Supponiamo di avere una terna di assi cartesiani, con il razzo che si muove lungo l’asse z; Le posizioni di Bill e George saranno quindi punti dell’asse z dipendenti dal tempo. Chiameremo z_B(t) la posizione di Bill e z_G(t) la posizione di George. Se al tempo zero George occupa la posizione z = 0 e la distanza verticale tra George e Bill è pari ad h, allora si avrà:

[0711111953]

[0711111954]

Bill emette il primo impulso luminoso al tempo t = 0; pertanto, invece di t₀ scriveremo semplicemente 0. Il tempo in cui il primo impulso è ricevuto è t₁. Il secondo impulso è emesso dopo un intervallo ∆t_B che è anche l’intervallo come misurato da Bill. George riceve il secondo impulso dopo un intervallo di tempo che egli misura come ∆t_G. Pertanto il tempo t₁ + ∆t_G è il tempo al quale il secondo intervallo è ricevuto.

La distanza percorsa dal primo impulso luminoso prima della sua ricezione è

[0711112001] z_B(0) – z_G(t₁) = c ⋅ t₁

dove ovviamente c è la velocità della luce. La distanza percorsa dal secondo impulso prima della sua ricezione è più corta, ed è data da:

[0711112002] z_B(∆t_B) – z_G(t₁ + ∆t_G) = c(t₁ + ∆t_G – ∆t_B)

Calcolando nella [0711112001] e nella [0711112002] z_G e z_B secondo le formule [0711111953] e [0711111954] e considerando trascurabili tutti i termini elevati al quadrato o a potenza superiore otteniamo:

[0711112005]

[0711112006]

Sottraendo membro a membro la [0711112006] dalla [0711112005] otteniamo:

[0711112010 ]

e cioè:

[0711120202 ]

e cioè:

[0711120205 ]

Tenendo conto della [0711112005], la quantità può essere scritta come:

[0711120150]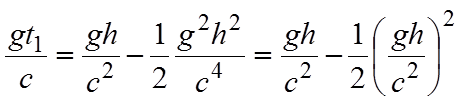

Trascurando termini dell’ordine di otteniamo:

[0711120208]

che sostituito nella [0711120205] dà:

[0711120209 ]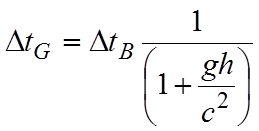

Considerato che è:

[0711120230 ]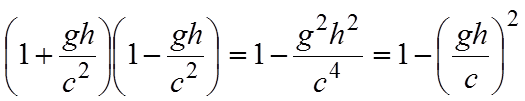

e che, essendo trascurabile si può scrivere:

[0711120231 ]

e cioè si può scrivere:

[0711120232 ]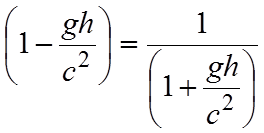

la [0711120209] equivale a:

[0711120233 ]

In altre parole, l’intervallo tra gli impulsi che viene misurato da George è approssimativamente più piccolo di un fattore rispetto all’intervallo misurato da Bill.

Se invece degli intervalli tra i segnali consideriamo la frequenza dei segnali otteniamo:

[0711112025 ]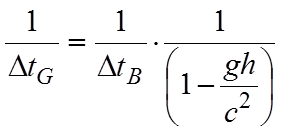

Dato che è:

[0711120234 ]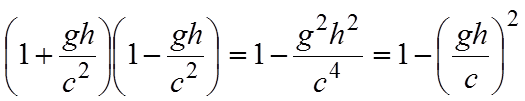

e, trascurando il termineè:

[0711120235]

e cioè:

[0711120236]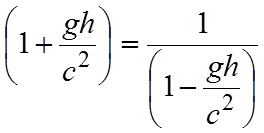

possiamo scrivere:

[0711120235]

che equivale a dire che:

[0711120237]

Per il principio di equivalenza, la [0711120237] deve valere anche in un campo gravitazionale. In un campo gravitazionale gh è proprio la differenza tra il potenziale gravitazionale Φ_B del punto in cui si trova Bill e il potenziale gravitazionale del punto Φ_G in cui si trova George:

Pertanto otteniamo, con buona approssimazione:

[0711120238]

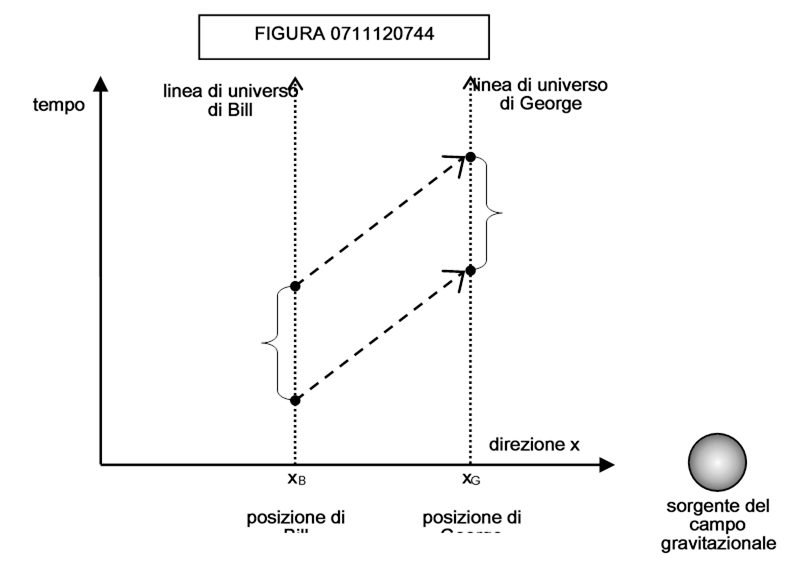
[0711120754]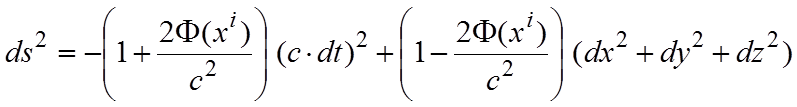

dove il potenziale gravitazionale Φ(xⁱ) dipende dalla posizione, ed è, per esempio intorno alla Terra, pari a

dove M_⊕ è la massa della Terra e G è la costante gravitazionale.

Nel 1919, uno dei più celebri esperimenti scientifici di tutti i tempi mostrò che l’idea dello spazio curvo non era solo una fantasia da matematici, ma un fatto della vita. Secondo la teoria della relatività generale di Einstein, pubblicata quattro anni prima, lo spazio è incurvato dalla gravità, e per questo la luce non viaggia sempre in linea retta, almeno non nel senso in cui Euclide avrebbe inteso il termine. L’effetto è troppo piccolo per essere percepito in condizioni normali, ma nel 1919 si presentò l’opportunità di un’eclisse totale di sole, visibile dall’Isola di Principe nel Golfo di Guinea. Nel corso dell’eclisse il fisico Arthur Eddington scattò una foto che mostrava come le stelle più prossime al sole non stessero esattamente dove avrebbero dovuto, proprio come previsto dalla teoria di Einstein. In altre parole, erano visibili, per la curvatura dei raggi di luce dovuta alla enorme forza gravitazionale del sole, delle stelle che non sarebbero state visibili se i raggi di luce fossero stati linee rette (figura 0705262039).

I fisici affermano che lo spazio è curvo localmente, perché è incurvato dalla forza di gravità. Stanno ancora discutendo per stabilire la struttura a grande scala dello spazio.

I cambiamenti di coordinate e la formula di distanza

back to index

Quando diciamo che uno spazio è euclideo se la metrica di Riemann è rappresentata dalla formula:

[0705271659] ds² = 1 ⋅ dx₁⋅ dx₁ + 1 ⋅ dx₂⋅ dx₂ +1 ⋅ dx₃⋅ dx₃

e cioè:

[0705312049] ds² = dx₁² + dx₂² + dx₃²

si impongono alcune precisazioni, perché uno spazio euclideo può essere coordinatizzato in modo tale che non vale la formula [0705312049]. Infatti, perché valga la formula occorre che i punti dello spazio (possiamo pensare allo spazio fisico) abbiano coordinate riferite a una terna di assi ortogonali con unità di lunghezza costituite da segmenti congruenti, cioè sovrapponibili per traslazione. In tal caso le coordinate, costituite ciascuna dalla distanza con segno del punto dagli assi, misurata secondo le unità dell’asse parallelo al segmento più breve tra il punto e l’asse, sono tali che la distanza definita tra i punti è quella euclidea.

Ma non in tutti i sistemi di coordinate possibili la formula della distanza è quella euclidea.

Cosa sono le coordinate? Dei numeri assegnati ai punti, si potrebbe rispondere in prima battuta.

Coordinatizzare un foglio vuol semplicemente dire dare un nome ai suoi punti. Dire punto (1,1) è dare semplicemente un nome costituito da numeri ad un oggetto chiamato “punto” che costituisce un elemento di una superficie spaziale^(0612110433).

Tuttavia, se fatta mediante assegnazione di numeri, l’operazione di coordinatizzazione non è solo, nelle intenzioni dei coordinatizzatori, l’assegnazione di un nomen, ma anche di una posizione reciproca dei punti, e cioè di una topologia.

Quindi normalmente la coordinatizzazione rispecchia una topologia.

Così, è vero che attribuendo ad una città 50° long. e 50° lat. e ad un’altra 30° long. e 20° lat. intendiamo esprimere anche l’idea che la prima città è più a est e più a sud di della seconda.

A ciascuna coppia di punti così individuati si può associare un numero detto distanza. Ripetiamo qui quanto detto sopra: la distanza può essere qualsiasi cosa, purché abbia tre caratteristiche: a) la distanza di un punto da se stesso è zero; b) la distanza tra due punti è sempre positiva; c) la distanza tra il punto p e il punto q è eguale alla distanza tra il punto q e il punto p; d) la somma della distanza tra p e q e della distanza tra q ed r deve essere non superiore alla distanza tra p ed r.

Non sempre esiste una diretta correlazione tra coordinate e distanza. Se coordinatizziamo un piano con coordinate ortogonali monometriche, sottraendo dalle coordinate (5,0) le coordinate (1,0) si ottiene la distanza di 4 effettivamente misurabile sul piano. Per usare le parole di Einstein, in questo caso “il differenziale delle coordinate fornisce direttamente la distanza”. Si dice che tali coordinate forniscono direttamente anche le distanze oblique, se si può utilizzare la formula di Pitagora.

Ma consideriamo ora altri esempi in cui la distanza non può essere ottenuta direttamente mediante sottrazione di coordinate o formule pitagoriche.

Come primo esempio, immaginiamo di introdurre nel piano un sistema di coordinate in cui l’unità di misura dell’asse y è doppia di quella dell’asse x. Allora, chiamati dx e dy le componenti di un displacement vector otteniamo la distanza mediante la formula:

ds² = dx² + 4dy²

che non è evidentemente la formula pitagorica. Possiamo anche adottare un sistema di coordinate affini, con assi non ortogonali e dotati di unità di misura non omogenee e coordinate misurate nel modo mostrato in figura 0705271728:

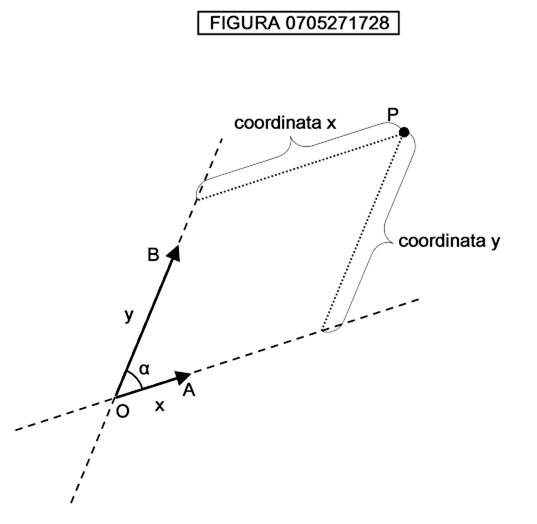
In tale figura le unità di ciascun asse sono di differente lunghezza: l’unità sull’asse x è OA e l’unità sull’asse y è OB. Il valore della coordinata x e della coordinata x è misurata lungo la parallela all’altro asse passante per il punto P considerato. Per calcolare la formula dell’elemento di distanza in tale sistema di coordinate osserviamo la figura 0705271757:

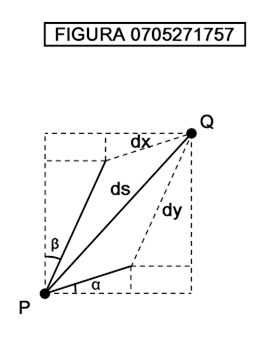
è abbastanza evidente che si ha:

ds = [(dx ‧ cos β + dy ‧ sin α)² + (dy ‧ cos α + dx ‧ sin β)²]^½

da cui:

ds² = dx² + dy² + 2‧(cos α ‧ sin β + sin α ‧ cos β) ‧ dx‧ dy

che, di nuovo, non è la distanza euclidea, anche se ci si trova in uno spazio euclideo. Esistono sistemi di coordinate diverse da quelle affini, chiamate coordinate curvilinee, come ad es. le coordinate sferiche (figura 0705271751).

In tale sistema di coordinate addirittura la formula della distanza è valida solo per spostamenti infinitesimali:

ds² = dx₁² + dx₂² + x₁² ⋅ dx₂² + x₁² ⋅ sin x₂² ⋅ dx₃²

Si può notare che in tale formula non euclidea compaiono le coordinate del punto considerato, e quindi essa varia da punto a punto.

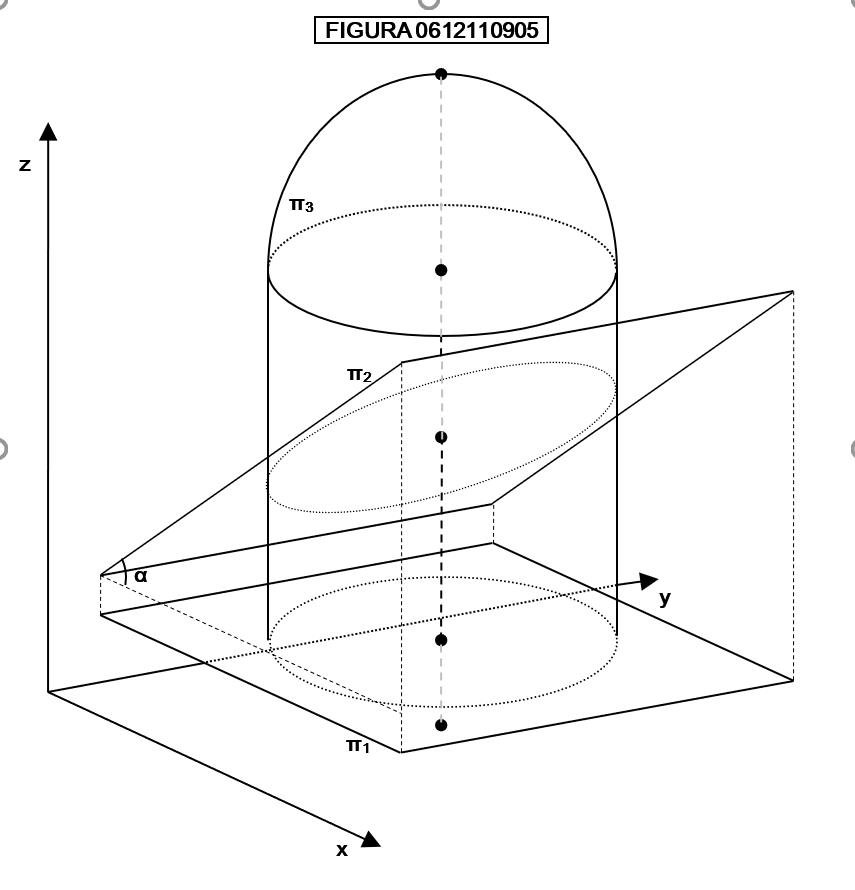
Osserviamo ancora la figura 0612110905; si vede come, coordinatizzando il piano π₁ mediante proiezione dei suoi punti sul piano xy la formula della distanza è quella euclidea:

d = √x² + y²

e cioè:

d² = 1 ⋅ x ⋅ x + 0 ⋅ x ⋅ y + 1 ⋅ y ⋅ y

Coordinatizzando invece lo stesso piano ruotato di un angolo α = 60° rispetto al piano xy la formula della distanza diviene:

d² = (2x)² + y²

mentre la coordinatizzazione della calotta π₃ sarà sempre del tipo:

d² = g₁₁ ⋅ x ⋅ x + g₁₂ ⋅ x ⋅ y + g₂₂ ⋅ y ⋅ y

ma con due importanti differenze: a) varierà da punto a punto (questo aspetto della questione sarà spiegato più avanti); b) non sarà possibile, mediante spostamenti della calotta, ottenere in nessun punto una formula della distanza di tipo euclideo..

In sintesi, tutte le misure della distanza sono rappresentate dalla formula generale:

d² = ∑_jk g_jk ⋅ x_j ⋅ x_k

(dove per semplicità, invece di utilizzare x, y, z, … ecc. si usano x₁, x₂, …, x_n) ma solo nel caso del piano è possibile operare uno spostamento nello spazio in modo che la formula della distanza sia quella euclidea.

In che modo possiamo allora stabilire se uno spazio sia euclideo? Per rispondere osserviamo che se lo spazio non è euclideo, allora non esiste una trasformazione di coordinate che conduca alla formula euclidea della distanza, mentre se lo spazio è euclideo, allora esiste una trasformazione che conduce alla formula euclidea.

la programmazione lineare e i politopi

Poligoni, poliedri, politopi

back to index

Prima di arrivare all’ultimo argomento di questa esposizione sulla importanza della geometria degli iperspazi, abbiamo bisogno di generalizzare il concetto di (iper)cubo definendo quegli oggetti multidimensionali limitati da (iper)superfici chiamati politopi convessi.

Ricordiamo che uno spazio zerodimensionale o 0-spazio è un punto, uno spazio 1-dimensionale o 1-spazio è una linea, uno spazio 2-dimensionale o 2-spazio è un piano, uno spazio 3-dimensionale o 3-spazio è lo spazio fisico in cui viviamo come descritto dalla geometria euclidea studiata a scuola.

Ricordiamo ancora che ogni spazio ha dei sottospazi, che sono precisamente gli spazi di dimensione minore in esso immersi.

Dalla definizione di iperpiano come luogo dei punti di uno spazio di n dimensioni le cui coordinate soddisfano una equazione lineare in n variabili possiamo individuare i seguenti iperpiani:

▸ Nello spazio monodimensionale formato da una linea l’iperpiano è un punto; l’equazione che ne individua le coordinate è del tipo:

ax = k

ovvero, in un linguaggio più omogeneo:

ax₁ = k

▸ Nello spazio bidimensionale del piano l’iperpiano è la linea; l’equazione che ne individua le coordinate è del tipo:

ax + by = k

ovvero, in linguaggio più omogeneo:

ax₁ + a₂x₂ = b

▸ Nello spazio tridimensionale l’iperpiano è una superficie. L’equazione che ne individua le coordinate è del tipo:

ax + by + cz = k

ovvero, in linguaggio più omogeneo:

a₁x₁ + a₂x₂ + a₃x₃ = b

▸ Nello spazio quadridimensionale l’iperpiano è uno spazio tridimensionale. L’equazione che ne individua le coordinate è del tipo:

a₁x₁+ a₂x₂ + a₃x₃ + a₄x₄ = b

Sia il punto, che la retta, che il piano hanno la caratteristica comune di dividere lo spazio in cui sono immersi (rispettivamente retta, piano, spazio tridimensionale) in due parti.

Dalle equazioni degli iperpiani si può notare che, fissate n-1 variabili, la n-esima risulta univocamente determinata; pertanto ogni punto di un iperpiano è individuato da (n-1) coordinate.

Gli iperpiani sono quindi i sottospazi (n-1)-dimensionali di uno spazio n-dimensionale.

Per definire i politopi partiamo dallo spazio bidimensionale (piano). In geometria piana si definisce poligono convesso una figura formata da una linea spezzata chiusa semplice (cioè senza lati non consecutivi intersecantesi) e dalla parte finita di piano da essa delimitata.

Un poligono convesso giace tutto da una stessa parte rispetto a ciascuna delle rette a cui appartengono i suoi lati. Un poligono non convesso, o poligono concavo, è invece diviso in due parti da almeno una retta cui appartiene uno dei suoi lati.

Un caso particolare di poligono è il poligono regolare un poligono che ha tutti i lati e tutti gli angoli congruenti (equiangolo ed equilatero). Esistono poligono regolari convessi e poligoni regolari non convessi.

L’analogo del poligono nello spazio tridimensionale è il poliedro. Un poliedro convesso è una figura solida delimitata da un numero finito di poligoni convessi, situati su piani diversi e tali che ognuno dei lati sia comune a due di essi e il piano di ciascuno lasci gli altri da una stessa parte.

Un poliedro regolare ha le facce costituite sono poligoni regolari congruenti e i suoi angoloidi sono congruenti tra loro.

Nello spazio tridimensionale ci sono, come ben sapevano gli antichi studiosi greci di geometria, solo cinque poliedri regolari: il tetraedro (con quattro facce costituite da triangoli equilateri), il cubo (sei facce costituite da quadrati), l’ottaedro (8 facce costituite da triangoli equilateri), il dodecaedro (12 facce costituite da pentagoni regolari) e l’icosaedro (20 facce costituite da triangoli equilateri).

D’ora in avanti, quando si parlerà di “poligono”, “poliedro” ecc. si intenderà sempre “poligono convesso”, “poliedro convesso” ecc.

Siamo ora pronti a definire l’equivalente di un poligono o di un poliedro in dimensioni più alte o più basse. Consideriamo a tale scopo la seguente successione:

▸ punto

▸ segmento

▸ poligono

▸ poliedro

……………

possiamo concludere che ciascuno di essi ha una definizione simile. Il termine generico di tale sequenza si definisce politopo convesso, ovvero una regione limitata (una porzione di spazio si dice limitata se non contiene nessuna semiretta) di uno spazio n-dimensionale delimitata da un numero finito di iperpiani, cioè di sottospazi (n-1)-dimensionali.

Una definizione alternativa di politopo convesso è quella di porzione di spazio n-dimensionale individuata dalla intersezione di un numero finito di semispazi che sia limitata, cioè non contenga alcuna semiretta

Secondo una terza definizione, più algebrica, un n-politopo convesso è definito da m equazioni del tipo:

a₁₁x₁+ a₁₂x₂ + … + a_1nx_n ≤ b₁

…………………………………

a_m1x₁+ a_m2x₂ + … + a_mnx_n ≤ b_m

I politopi convessi hanno altre caratteristiche distintive che qui non stiamo a definire:

▸ le iperfacce sono formate da sottospazi n-1 dimensionali (gli iperpiani)

▸ Le iperfacce sono a loro volta politopi convessi di dimensione n-1

▸ due qualsiasi iperfacce hanno in comune uno e un solo “spigolo”, costituito da un sottospazio (n-1)-dimensionale

▸ due iperfacce non si intersecano, cioè non hanno in comune altri punti oltre quelli dello “spigolo”

▸ il politopo non è costituito esclusivamente da un insieme di iperfacce

▸ è possibile passare da una iperfaccia ad una qualsiasi altra attraverso una sequenza di iperfacce

▸ due iperfacce non giacciono mai sullo stesso iperpiano

▸ il politopo non è mai contenuto in un iperpiano o in altro sottospazio di minore dimensione.

▸ L’iperpiano di ogni iperfaccia lascia tutte le altre iperfacce da una stessa parte

Le facce di un politopo quadridimensionale sono poliedri a tre dimensioni. Per un politopo regolare questi poliedri devono a loro volta essere regolari, e la disposizione delle facce deve essere la stessa a ciascun vertice. Ne risulta che ci sono solo sei politopi quadridimensionali regolari: il simplesso, che ha per facce cinque tetraedri, l’ipercubo,con otto facce cubiche, la 16-cella, delimitata da 16 tetraedri, la 24-cella, con 24 ottaedri, la 120-cella, con 120 dodecaedri e la 600-cella, con 600 facce costituite da altrettanti tetraedri.

Per dimensione di un politopo convesso si intende la dimensione del minimo sottospazio che lo contiene. Ad esempio un poligono collocato nello spazio reale a tre dimension va considerato come un 2-politopo.

Possiamo così considerare la seguente sequenza di politopi in base alla dimensione n:

▸ Nullitopo (n = -1)

▸ Monade (n = 0)

▸ Diade (n = 1)

▸ Poligono (n = 2)

▸ Poliedro ( n = 3)

Politopi e programmazione lineare

back to index

La ricerca operativa ebbe origine con la seconda guerra mondiale, e usa metodi matematici epr affrontare problemi complessi che implicano la direzione e la conduzione di grandi sistemi di uomini, macchine, materiali e denaro nel campo dell’industria, del commercio, del governo e della difesa.

La programmazionelineare è una tecnica usata per fornire una descrizione matematica, ovvero un modello, di un problema della vita reale in cui qualcosa deve essere massimizzato (ad esempio i profitti o la sicurezza) o minimizzato (ad esempio i costi o i rischi). L’ottimizzazione richiesta si raggiunge con una opportuna scelta di valori di un certo numero di parametri, ovvero di variabili. Entrambi i fattori da ottimizzare o alcuni o tutti i parametri saranno passibili di uno o più vincoli. La parola “lineare” indica che tutte le espressioni matematiche del modello sono lineari,cioè non comportano la moltiplicazione di due o più variabili tra di loro o il loro elevamento a potenza. Nella pratica, questa limitazione non è rilevante, dal momento che la maggior parte dei problemi incontrati nella vita reale sono intrinsecamente lineari, o possono essere supposti tali senza generare errori di qualche entità.

Un primo esame del problema rivela che i vincoli lineari hanno una rappresentazione geometrica naturale. I valori delle variabili che soddisfano tutti i vincoli corrispondono ai punti che giacciono entro una determinata figura geometrica: se le variabili sono due, quella figura sarà un poligono il cui numero di lati corrisponde al numero dei vincoli; se le variabili sono tre, sarà un poliedro; se sono n, sarà un politopo in uno spazio n-dimensionale. Naturalmente è impossibile disegnare un politopo a quattro o più dimensioni, mai procedimenti matematici restano semplici qualunque sia la dimensionie.

Basterà un esempio elementare per chiarire quanto si è detto.

Immaginiamo la ditta Alfa che produce due tipi di sciarpe multicolori, A e B. Per ogni sciarpa vanno usate lane di tre colori, rosso, verde e giallo, per ottenere l’effetto multicolore. La quantità di lana occorrente per una sciarpa di ciascun tipo di tessuto e la quantità totale di lana di cui si dispone per ciascun colore sono indicate nella tabella 0705241722.

tabella 0705241722
Colore della lana	Quantità occorrente per sciarpa		Quantità disponibile
Colore della lana	Sciarpa A	Sciarpa B	Quantità disponibile
Rosso	4 kg	4 kg	1400 kg
Verde	6 kg	3 kg	1800 kg
Giallo	2 kg	6 kg	1800 kg

Il profitto del fabbricante è di 12 euro su ciascuna sciarpa di tessuto A e di 8 euro su ciascuna sciarpa di tessuto B. La domanda che ci poniamo è come debba essere usata la lana disponibile per massimizzare il profitto totale.

Sia x il numero di sciarpe di tessuto A prodotte e y il numero di sciarpe di tessuto B prodotte. Il profitto P, espresso in euro, sarà dato da

[1] P = 12x + 8y

Quali sono i vincoli sui valori di x e y? Poiché si hanno solo 1400 kg di lana rossa e tutti e due i tipi di sciarpa richiedono 4 kg di lana rossa per ogni sciarpa dovrà essere:

[2] 4x + 4y ≤ 1400

Allo stesso modo, considerando la lana verde e gialla di cui si dispone si avrà:

[3] 6x + 3y ≤ 1800

[3] 2x + 6y ≤ 1800

Infine, poiché né x né y dovrebbero essere negativi (vincolo che è ovvio quando si considera il problema reale, ma che deve essere reso esplicito nella rappresentazione matematica), valgono le condizioni:

[4] x ≥ 0

[4] y ≥ 0

Abbiamo quindi le tipiche disequazioni che, come abbiamo visto, costituiscono una delle definizioni di poligono convesso:

4x + 4y ≤ 1400

6x + 3y ≤ 1800

2x + 6y ≤ 1800

- x ≤ 0

- y ≤ 0

La figura 0705241735 offre una rappresentazione grafica dei vincoli imposti dalle disuguaglianze [2], [3], [4].

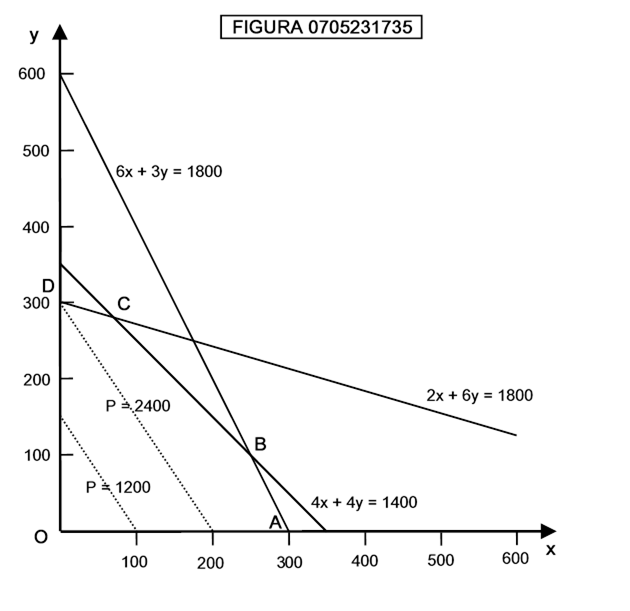
Qualsiasi coppia di valori che soddisfi tutti questi vincoli costituirà le coordinate di un punto all’interno della regione vincolare ODCBA, e viceversa qualsiasi punto in quest’area avrà coordinate che soddisfano le disuguaglianze [2], [3], [4].

La figura 0705250616 riporta l’area eliminando le linee al difuori di essa:

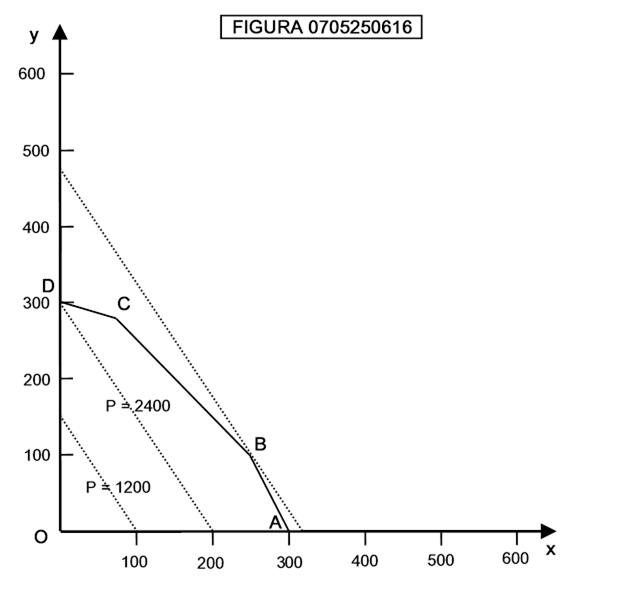
Ora dobbiamo trovare un punto dentro la regione vincolare ODCBA che renda la quantità P dell’equazione [1] il più grande possibile.

Tutte le rette con equazioni della stessa forma della [1], per un valore fissato di P, sono parallele tra loro. Tre di queste, la retta che rappresenta un profitto di 1200, quella che rappresenta un profitto di 2400 e la retta che passa per B, sono tratteggiate nella figura 0705241735. E’ dunque abbastanza chiaro cosa si deve fare per massimizzare P: spostare la retta del profitto (data dalla [1]) il più lontano possibile dall’origine senza uscire del tutto dalla regione vincolare ODCBA. La retta limite è quindi quella che passa per B. Le coordinate di B si ottengono facilmente con l’algebra elementare, come soluzione di un sistema di due equazioni:

6x + 3y = 1800

4x + 4y = 1400

La soluzione è 250 sciarpe di tessuto A e 100 sciarpe di tessuto B. Quindi il fabbricante deve produrre 250 sciarpe di tessuto A e 100 di tessuto B. In tal modo il profitto ottenuto, che è il massimo possibile, sarà appunto di:

P = 12x + 8y = 12 ⋅ 250 + 8 ⋅ 100 = 3800 €

Verrà così usata tutta la lana rossa e tutta la verde, mentre ne avanzeranno 700 kg di quella gialla (e risulterà quindi che il fabbricante non ha fatto bene i suoi calcoli prima).

Ora che il problema è stato risolto, vediamo di analizzarlo. I vincoli erano rappresentati nella figura 0705241735 tramite la regione poligonale ODCBA del piano. Il punto di massimo era uno dei vertici del poligono, e rimaneva da stabilire quale dei cinque. Si noti che il punto di massimo è sempre uno dei vertici anche se cambia la equazione [1], perché, anche nel caso limite in cui la retta rappresentata dall’equazione abbia inclinazione eguale a uno dei lati, allora tutto il lato darebbe lo stesso profitto, e potrebbe essere scelto una delle sue due estremità.

In questo semplice esempio non era difficile da trovare, eppure è proprio questo il punto che rende complicati i problemi di programmazione lineare più complessi, e di conseguenza più realistici. In un problema con tre variabili, i vincoli daranno origine a un poliedro tridimensionale; con n variabili si otterrà un politopo n-dimensionale, che non si può disegnare ma che può ancora essere trattato algebricamente. In ogni caso il problema si riduce a trovare il vertice della regione vincolare (poligono, poliedro o politopo) in cui si verifica l’ottimizzazione.

Non è difficile passare da un esempio bidimensionale, dove la regione vincolare è un poligono, ad un esempio tridimensionale, dove la regione vincolare è un poliedro. Consideriamo l’impresa Beta, che produce tre diversi tipi di sciarpa multicolore, A, B, C, utilizzando per ciascun tipo lana rossa e lana verde. La tabella 0705242154 mostra quanta lana di ciascun colore è necessaria per ottenere ciascuno dei tre tipi di sciarpa e quanta lana di ciascun tipo è in magazzino:

tabella 0705242154
Colore della lana	Quantità occorrente per sciarpa			Quantità disponibile
Colore della lana	Sciarpa A	Sciarpa B	Sciarpa C	Quantità disponibile
Rosso	4 kg	4 kg	4 kg	1200 kg
Verde	12 kg	6 kg	6 kg	2400 kg

I vincoli che definiscono il poliedro convesso che costituisce la regione vincolare sono:

4x + 4y + 4z ≤ 1200

12x + 6y + 6z ≤ 2400

- x ≤ 0

- y ≤ 0

- z ≤ 0

La funzione del profitto è:

P = 30x + 12y + 10z

Nella figura 0705232046 vengono indicate le porzioni di piano che corrispondono a tali vincoli. Il piano che passa per i punti F, D, E rappresenta il vincolo 12x + 6y + 6z = 2400. Il piano che passa per i punti C, A, B rappresenta il vincolo 4x + 4y + 4z ≤ 1200. Essi si intersecano lung la linea GH.

Nella figura 0705232127 abbiamo evidenziato la regione vincolare eliminando le parti di piano al difuori di essa. Come si vede si tratta di un poliedro convesso le cui facce sono i poligoni convessi OAF, FGH, HGAB, FOB.

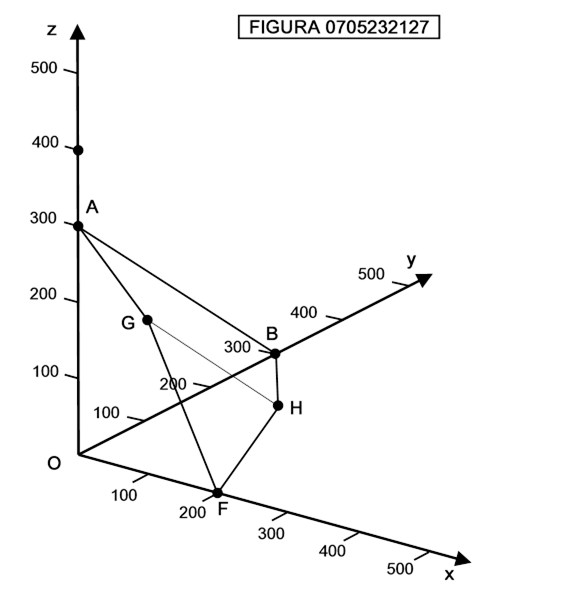
Nella figura 0705232130 vengono riportati, in linea tratteggiata, il piano che passa per i punti L,A,M e il piano che passa per i punti F,P,N. Si tratta rispettivamente del piano dei punti che rappresentano combinazioni x,y,z che forniscono un profitto di 3000 euro e del piano dei punti che rappresentano combinazioni x,y,z che forniscono un profitto di 6000 euro. Come si vede, il piano individuato da F,P,N è quello in posizione limite: piani con profitti superiori risulterebbero fuori dalla regione vincolare del poliedro. Tale piano ha in comune con la regione vincolare il punto F, che quindi è il vertice del poliedro che fornisce il massimo profitto totale (6000 euro).

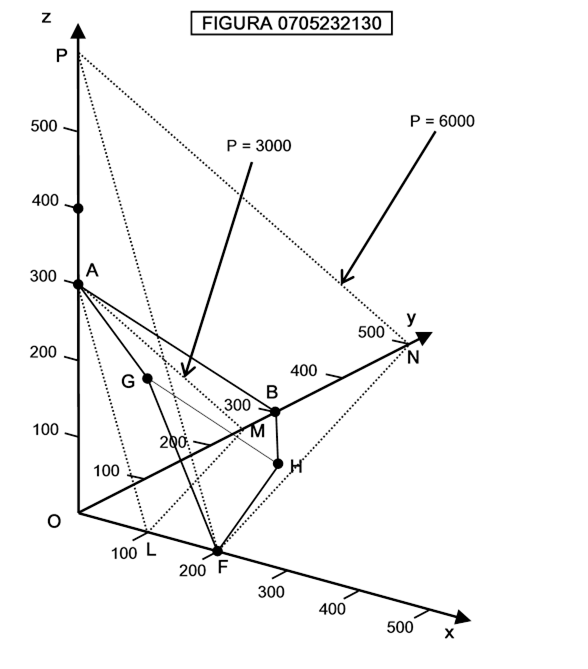
Come si vede, in ogni caso il problema si riduce a trovare il vertice della regione vincolare (poligono, poliedro o politopo) in cui si verifica l’ottimizzazione.

Come si può fare? Potrebbero esserci milioni di vertici, per cui una ricerca sistematica è di solito fuori discussione. Occorre quindi un metodo diverso.

Nel 1947 il matematico americano George Dantzig ne ideò uno: l’algoritmo del simplesso.

Un algoritmo è un insieme di istruzioni per la manipolazione di dati, che consente di ottenere altri dati e che può essere eseguito da una macchina non-inteligente, come un computer. Ad es. le istruzioni per la divisione tra due numeri o per l’estrazione di radice sono algoritmi. Un programma di computer per addizionare due numeri è un algoritmo. L’algoritmo si differenzia da una operazione mtematica, come l’addizione o la moltiplicazione, che pure può essere compiuta da una macchina non-intelligente, come una calcolatrice tascabile, perché è composto da passi successivi.

In pratica, con questo metodo si parte da un vertice (qui non diremo come si trova questo vertice iniziale) e poi ci si sposta sulla superficie del politopo, lungo i lati, da vertice a vertice. Ogni volta che si arriva a un vertice, ci saranno varie direzioni in cui procedere e vari criteri per decidere quale di queste scegliere. Il più ovvio consiste nel portarsi a un vertice che aumenta la quantità da massimizzare, o la diminuisce se è da minimizzare.

Esiste un metodo più veloce? Potremmo pensare, invece di muoverci sulla superficie, di “abbreviare” seguendo un percorso all’interno del politopo. Il primo di questi metodi è stato messo a punto nel 1976 da un gruppo di matematici sovietici. Prende il nome di “metodo ellissoidale” perché si serve di una serie di ellissoidi che approssimano il politopo. Purtroppo questo metodo è alquanto lento.

Un secondo metodo basato su percorsi interni, molto più veloce del metodo ellissoidale, e tale da competere con successo con l’algoritmo del simplesso fu trovato nel 1984 da un ventottenne ricercatore nei laboratori Bell, Narendra Karmarkar. L’algoritmo di Karmarkar utilizza una matematica avanzatissima per generare trasformazioni del politopo che consentano di invidivuare velocemente un percorso al suo interno. L’algoritmo di Karmarkar mostra come gli ultimi sviluppi delle teorie matematiche sugli spazi multidimensionali possano essere applicate con successo a problemi pratici.