Introduzione divulgativa ai tensori

 

La redazione di questo documento verrà gradualmente completata entro il 2008

 

back to HomePage

 

❍ Lo spazio vettoriale

❍ Lo spazio euclideo

❍ Le trasformazioni di coordinate

❍ La definizione analitica dei vari tipi di tensori come systems che variano al variare delle coordinate

❍ Operazioni tra tensori

❍ Esempi di systems tensoriali

❍ Tensori e manifolds: gli spazi tangenti

❍ La formalizzazione algebrica astratta dei tensori

❍ Approfondimenti di teoria algebrica astratta dei tensori

 

 

 

❍ Lo spazio vettoriale

back to index

 

Lo spazio vettoriale è uno spazio astratto, dove i punti o “vettori” u, v, w,… sono enti di qualsiasi genere che soddisfano i seguenti assiomi:

 

▸    u + (v + w) = (u + v) + w

 

▸    u + v = v + u

 

▸    Esistenza di un elemento tale che v + 0 = v

 

▸    1 ⋅ v = v

 

▸    h ⋅ (k ⋅ v) = (h ⋅ k) ⋅ v

 

▸    k ⋅ (v + w ) = k ⋅ v + k ⋅ w

 

dove h, k sono numeri reali o complessi o elementi di strutture analoghe, chiamate campi  e 1 è l’elemento neutro del campo.

La relazione col tipo di campo viene di solito esplicitata parlando di K-spazi vettoriali (R-spazi, C-spazi, ecc.)

Un esempio familiare di spazio vettoriale è lo spazio dei vettori liberi  tridimensionali della fisica, che possiamo raffigurare come una “palla” irta di vettori che hanno il loro punto iniziale (o punto di applicazione) in una origine comune. Le copie di tali vettori applicate a questo o quel punto dello spazio, definiti vettori applicati, rappresentano in realtà un unico vettore libero, di cui hanno la stessa direzione, lo stesso verso e la stesso modulo o grandezza (lunghezza)

Un altro esempio, meno intuitivo, di spazio vettoriale, è quello delle enople di numeri con l’addizione componente per componente e la moltiplicazione scalare.

Esiste lo spazio vettoriale delle funzioni su insiemi (es. spazio di Banach), lo spazio vettoriale dei polinomi in x, lo spazio vettoriale delle matrici ecc.

La dimensione di uno spazio vettoriale è il numero minimo di vettori linearmente indipendenti {b_i} necessari per esprimere ogni vettore dello spazio come loro combinazione lineare:

 

v = v₁ ⋅ b₁ + v₂ ⋅ b₂ + … + v_n ⋅ b_n

 

dove v_i (i = 1,…,n) non è un vettore ma uno scalare chiamato i-esima componente del vettore v nella base b.

 

 

❍ Lo spazio euclideo

back to index

 

Uno spazio euclideo è uno spazio affine su un K-spazio vettoriale V nel quale è definito un prodotto scalare.

Usualmente si utilizza una definizione meno generale, intendendosi per spazio euclideo l’n-spazio euclideo numerico, cioè lo spazio affine numerico Aⁿ(R) dotato del prodotto scalare standard.

Si tratta dello spazio vettoriale Rⁿ costituito dall’insieme delle n-ple di numeri reali tra due punti qualsiasi del quale è definito un vettore differenza o displacement vector o vettore applicato costituito semplicemente dalla differenza componente per componente tra le due enople considerate. In tal modo, ad ogni punto di Rⁿ risulta associato uno spazio tangente, che è uno spazio vettoriale, isomorfo ad Rⁿ, costituito da tutti i vettori differenza che hanno come secondo termine della sottrazione il vettore considerato.

Il prodotto scalare standard tra due enople X = (x₁,…,x_n) ed Y = (y₁,…,y_n) è definito come lo scalare

 

X ⋅ Y = x₁ ⋅ y₁ + … + x_n ⋅ y_n

 

Questo prodotto consente di dotare lo spazio euclideo della misura di lunghezze, distanze ed angoli, ciò di cui è sprovvisto lo spazio vettoriale.

La lunghezza o norma di un vettore v = (v₁,…,v_n) è definita come:

 

 

La distanza tra due vettori è definita come la norma del loro vettore differenza

L’angolo θ tra due vettori è definito dalla relazione:

 

 

 

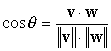
❍ Le trasformazioni di coordinate

back to index

 

Dato uno spazio euclideo E di dimensione n, e una funzione:

 

f : E ➙ Rⁿ

 

questa costituisce un sistema di coordinate per E se è bijettiva e di classe C² (cioè possiede derivate prime e seconde continue in tutta E).

Un sistema di coordinate è definito cartesiano (sinonimi: rettangolare, cartesiano rettangolare) se la distanza tra due punti arbitrari P(x¹,…,xⁿ) e Q(y¹,…,yⁿ) è la cosiddetta distanza euclidea, data da:

 

PQ = √(x¹ – y¹)² + … + (xⁿ – yⁿ)²

 

Dati due sistemi di coordinate f₁ e f₂, Una bijezione

 

f₁^-1 ∘ f₂ : Rⁿ ➙ Rⁿ

 

costituisce una trasformazione di coordinate, definita dalle n equazioni:

 

                        y₁ = y₁(x₁,…,x_n)

[0802062242]       .........................

                        y_n = y_n(x₁,…,x_n)

 

Nel caso di trasformazioni lineari di coordinate le equazioni assumono la forma:

 

                            y₁ = a₁₁ ⋅ x₁ + … + a_1n ⋅ x_n

[0802062245]           …………………..............

                            y_n = a_n1 ⋅ x₁ + … + a_nn ⋅ x_n

 

e la matrice:

 

[0802062247]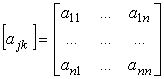 

 

è detta matrice di trasformazione delle coordinate.

Queste equazioni possono essere interpretate in due modi: secondo l’interpretazione detta alibi  si tratta di una trasformazione nel piano che assegna ad un punto un altro punto; secondo l’interpretazione alias si tratta di una trasformazione di coordinate, che assegna allo stesso punto coordinate diverse.

L’interpretazione alibi dà origine allo studio dei gruppi di trasformazione  (ad es. nel piano e nello spazio tridimensionale): una branca affascinante della matematica (le impronte di un essere umano che cammina sulla sabbia o alcuni steli di piante dove le foglie appaiono a intervalli regolari dopo aver coperto la medesima frazione di un cerchio completo attorno al gambo possiedono la simmetria nota come glissoriflessione, che è un tipo di roto-traslazione bi- o tridimensionale)

Il grande geometra dell’800 Felix Klein, nel famoso Programma di Erlangen indicò come classificare i vari tipi di geometrie in base alle proprietà invarianti per determinati gruppi di trasformazione. La trasformazione affine più generale da lui proposta, la trasformazione proiettiva, è quella:

 

 

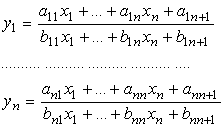
lo studio dei cui invarianti ha dato origine alla geometria proiettiva .

Si definiscono trasformazioni affini  quelle che considerano solo i numeratori della trasformazione lineare generale:

 

                        y₁ = a₁₁ ⋅ x₁ + … + a_1n ⋅ x_n + b₁

[0802070940]       …………………......................

                        y_n = a_n1 ⋅ x₁ + … + a_nn ⋅ x_n + b_n

 

Sono trasformazioni affini le rotazioni, le traslazioni e i ribaltamenti. Esse non conservano in generale né distanze né angoli.

Le trasformazioni lineari omogenee del tipo:

 

                        y₁ = a₁₁ ⋅ x₁ + … + a_1n ⋅ x_n

[0802070945]       …………………...............

                        y_n = a_n1 ⋅ x₁ + … + a_nn ⋅ x_n

 

corrispondono a delle rototraslazioni degli assi (possiamo chiamarle trasformazioni cartesiane) e conservano distanze (cosiddette isometrie) ed angoli.

Nel caso di trasformazioni non lineari delle coordinate, dette trasformazioni curvilinee, di formula generica:

 

                        y₁ = f₁(x₁, … , x_n)

[0802070950]       …………………...

                        y_n = f_n(x₁, … , x_n)

 

non vengono in generale conservati né distanze né angoli né proprietà proiettive. In ogni punto può essere calcolata la matrice delle derivate prime:

 

[0802062249]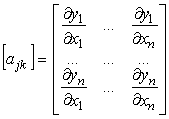 

 

Se si interpretano le formule [0802070950] come formule di un endomorfismo Rⁿ ➙ Rⁿ (cosiddetta interpretazione alibi della trasformazione) anziché come formule di un cambiamento di coordinate (cosiddetta interpretazione alias della trasformazione) allora tale matrice [0802070950] non è altro che la matrice jacobiana della trasformazione. Si noti che nel caso di trasformazioni lineari la matrice [0802070950] è essa stessa la matrice delle derivate prime.

 

 

❍ La definizione analitica dei vari tipi di tensori come systems che variano al variare delle coordinate

back to index

 

La nozione di tensore costituisce la naturale generalizzazione di quella di vettore.

Consideriamo dapprima il caso più semplice di una trasformazione lineare di coordinate. Dato un vettore V, definito dall’enopla (x₁,…,x_n) nel sistema di coordinate X, esso sarà definito da una diversa enopla (y₁,…,y_n) nel sistema di coordinate Y. Pensiamo in particolare ad un displacement vector: il modo più naturale per identificarlo attraverso i cambiamenti di coordinate sarà quello di definirlo come un sistema di n numeri che al cambiare delle coordinate cambia con la stessa legge di trasformazione delle coordinate. In termini matriciali si ha:

 

[0802062251]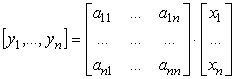 

 

Un vettore è così un system covariante (di numeri) o tensore covariante di ordine 1. Il termine covariante si riferisce al fatto che la matrice della sua trasformazione ha gli stessi valori di quella di trasformazione delle coordinate.

In termini analitici, la legge di trasformazione è la seguente:

 

[0802070929]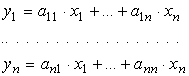 

 

Considerando che le a_jk non sono altro che le derivate parziali della trasformazione possiamo scrivere:

 

[0802070931]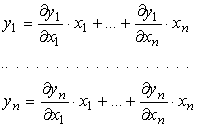 

 

ovvero, espressa in modo più compatto con la cosiddetta convenzione di Einstein:

 

[0802062255] 

 

dove si intende che due indici identici, uno in alto e uno in basso, vanno sommati per tutti i loro valori.

Oltre ai displacement vectors vi sono molte altri systems di numeri che variano con la legge [0802062255]: si pensi alle stesse coordinate.

Spesso la parola tensore non sta ad indicare un unico system, ma un campo tensoriale, cioè una funzione continua

 

f : (R^*)^r ⊗ R^s ➙ E

 

dallo spazio dei tensori di tipo (s,r) allo spazio euclideo E, che assegna ad ogni punto di E un tensore.

Consideriamo ora una trasformazione curvilinea (cioè non necessariamente lineare) di coordinate. Non sarà più possibile esprimere il displacement vector  come oggetto che si trasforma secondo la [0802062255], neppure considerando una diversa matrice di trasformazione per ogni punto, poiché vettori diversi (anche semplicemente di lunghezza) applicati nel medesimo punto daranno displacements diversi nel nuovo sistema di coordinate.

I systems che, come i displacement vector, variano con la legge [0802062255] in relazione ad una trasformazione lineare omogenea di coordinate ma non in relazione a trasformazioni non lineari o lineari non omogenee fanno parte della categoria dei tensori cartesiani; i systems che variano con la legge [0802062255] in relazione ad una trasformazione lineare non omogenea di coordinate ma non in relazione ad una trasformazione curvilinea fanno parte della categoria dei tensori affini; i systems che variano con la legge [0802062255] in relazione a trasformazioni generali di coordinate, incluse quelle curvilinee fanno parte della categoria dei tensori generali o “tensori” senza aggettivi.

Un esempio di tensore affine che però non è un tensore rispetto a trasformazioni generali di coordinate è dato dalla ordinaria derivazione parziale di un campo tensoriale. Rispetto a cambiamenti affini di coordinate l’insieme degli nⁿ numeri che costituiscono le n derivate parziali per ognuno degli n componenti di un vettore controvariante si trasformano con legge tensoriale, ma non così quando il cambiamento di coordinate è curvilineo. In questo caso alla differenziazione ordinaria si sostituisce la cosiddetta derivazione covariante, su cui vedi più avanti.

Mentre per i tensori cartesiani non si distinguono tensori covarianti e controvarianti, perché sono identici, per i tensori generali è della massima importanza distinguerli secondo la legge di variazione. Diamo pertanto le seguenti definizioni generali:

 

▸    Tensori covarianti e controvarianti del primo ordine

Si supponga che in qualche regione S di ℝn siano definiti due sistemi di coordinate, e che questi due sistemi siano connessi da equazioni della forma:

 

 

La funzione a valori reali x̅ⁱ(x) è definita una “trasformazione di coordinate” se è bijettiva e di classe C² (cioè che possiede derivate seconde continue in tutta S).

Questo si esprime anche dicendo che il dominio della funzione x̅ⁱ(x) rappresenta un sistema (ammissibile) di coordinate del generico punto x come definito nel sistema (xⁱ) nella regione S di ℝⁿ

Si consideri un campo vettoriale V = (Vⁱ) definito su un sottoinsieme S di ℝⁿ [cioè, per ogni i, il componente Vⁱ = Vⁱ(x) è un campo scalare (funzione a valori reali) con x che varia in S]. In ogni sistema di coordinate legato al sistema considerato da una trasformazione ammissibile che contenga S, siano Vⁱ,…,Vⁿ espressi da funzioni a valori reali delle coordinate:

 

Tⁱ(x¹,…,xⁿ)       nel sistema (xⁱ)

T^̅i(x̅ⁱ,…, x̅ⁿ)       nel sistema (x̅ⁱ)

 

Il campo vettoriale V è un tensore controvariante di ordine uno se le sue componenti (Tⁱ) e (T^̅i) relative rispettivamente ai sistemi (xⁱ) e (x̅ⁱ) obbediscono alla legge di trasformazione:

 

 

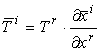
dove le sono le derivate parziali della trasformazione di coordinate.

Il campo vettoriale V è un tensore covariante di ordine 1 se le sue componenti (T_i) e (T^̅_i) relative rispettivamente ai sistemi (xⁱ) e (x^̅i) obbediscono alla legge di trasformazione:

 

 

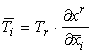
dove le sono le derivate parziali della trasformazione inversa di coordinate.

 

▸    Tensori del secondo ordine covarianti, controvarianti e misti

Si supponga che V = (V^ij) denoti un campo di matrici; cioè (V^ij) è una matrice di nxn campi scalari V^ij(x), tutti definiti sulla stessa regione U = {x} in ℝⁿ.

Si supponga che in due sistemi (xⁱ) e (x̅ⁱ) V abbia una rappresentazione (T^ij) e (T^̅ij) rispettivamente, dove (xⁱ) e (x̅ⁱ) sono sistemi ammissibili di coordinate.

Il campo matriciale V è un tensore controvariante di ordine due se le sue componenti (T^ij) in (xⁱ) e (T^{̅ ij}) in (x̅ⁱ) obbediscono la legge di trasformazione:

 

 

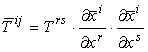
Il campo matriciale V è un tensore covariante di ordine due se le sue componenti (T_ij) in (xⁱ) e (T^̅_ij) in (x̅ⁱ) obbediscono alla legge di trasformazione:

 

 

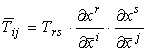
Il campo matriciale V è un tensore misto di ordine due, controvariante di ordine uno e covariante di ordine uno  se le sue componenti (T_j^I) in (xⁱ) e (T^̅_j^I) in (x̅ⁱ) obbediscono alla legge di trasformazione:

 

 

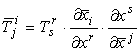
▸    Tensori di ordine arbitrario

Si consideri un campo vettoriale generalizzato, che è un array ordinato di n^m (m = p + q) campi scalari, definito su una regione U in ℝⁿ e le cui componenti siano denotate come:

 

 

 

nei due rispettivi sistemi di coordinate (xⁱ) e (x̅ⁱ)

Tale campo vettoriale è un tensore di ordine m = p + q, controvariante di ordine p e covariante di ordine q se le sue componenti in (xⁱ) e in (x̅ⁱ) obbediscono alla legge di trasformazione:

 

 

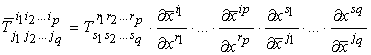
dov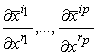e  le  e le 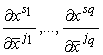 sono le derivate della trasformazione e della sua inversa

 

▸    Tensori di ordine zero (campi scalari)

Data una funzione su Rⁿ che costituisce un campo di scalari, essa viene considerata come un tensore di ordine zero.

 

                                                                                                                                            

❍ Operazioni tra tensori

back to index

 

▸    Addizione e sottrazione di tensori

Occorre che i tensori siano dello stesso tipo: un tensore di tipo (r,s) può essere sommato solo ad un tensore di tipo (r,s). Non è nemmeno possibile addizionare tensori definiti su punti differenti di un manifold.

La somma (sottrazione) si ottiene sommando (sottraendo) i due tensori componente per componente

 

▸    Moltiplicazione di un tensore per uno scalare

Si moltiplica ciascun componente del tensore per lo stesso scalare

 

▸    Moltiplicazione esterna (outer product) di due tensori

Se i due tensori sono dati da:

 

S_ij^kl

 

T_rs^tu

 

e chiamiamo il loro prodotto:

 

M_ijrs^kltu = S_ij^kl ⋅ T_rs^tu

 

allora si avrà ad esempio:

 

M₂₅₄₆¹³⁷⁸ = S₂₅¹³ ⋅ T₄₆⁷⁸

 

Come si vede, dalla moltiplicazione si ottiene un tensore il cui ordine è la somma degli ordini dei tensori moltiplicati. Nell’esempio di cui sopra, M è un tensore di ordine 8, covariante di ordine 4 e controvariante di ordine 4, poiché risulta dalla moltiplicazione di due tensori ciascuno di ordine 4, covariante di ordine 2 e controvariante di ordine 2.

Se ogni indice può assumere n valori, il prodotto esterno può essere pensato come l’operazione di moltiplicare, per ogni valore del system S_ij^kl gli n⁴ valori del system T_rs^tu

Esiste una certa ambiguità dovuta all’ordine della moltiplicazione: se avessimo definito invece:

 

M_rsij^tukl = T_rs^tu ⋅ S_ij^kl

 

avremmo avuto:

 

M₂₅₄₆¹³⁷⁸ = T₂₅¹³ ⋅ S₄₆⁷⁸

 

che è un valore in generale diverso.

Non si considerano separatamente gli indici superiori e inferiori; occorre tenere presente che un tensore è un unico sistema di valori (system) indicizzato sia dagli indici superiori che da quelli inferiori.

L’unica differenza tra un tensore misto di tipo (1,1) e un tensore di ordine (2,0) o (1,0) è nella legge di cambiamento delle componenti (vedi luogo citato).

Quindi occorre prendere un singolo scalare indicizzato dagli indici del primo tensore, e moltiplicarlo per tutti gli scalari indicizzati dagli indici del secondo tensore secondo una moltiplicazione "componentwise"

Componentwise multiplication vuol dire che

 

T^jk_lm ⋅ S^pq_ru = W^jkpq_lmru

 

E’ facile dimostrare che il prodotto di due tensori è ancora un tensore, cioè soddisfa alla legge di trasformazione tensoriale

Scriveremmo forse cosa più esatta se scambiassimo i membri e sostituissimo al segno di eguale il segno di vero per definizione:

 

W^jkpq_lmru ≡ T^jk_lm ⋅ S^pq_ru

 

da cui segue che la legge di variazione dei componenti del tensore è rispettata, e quindi si tratta di un tensore.

Consideriamo il caso più semplice di un tensore T¹₀ e di un tensore S⁰₁:

 

W^r_s ≡ T^r₀ ⋅ S⁰_s ≡ T^r ⋅ S_s

 

che funziona da forma bilineare su V*xV:

 

W(f,v) = f_r ⋅ v^s ⋅ W^r_s

 

che è quanto dire una moltiplicazione matriciale

 

[f] ⋅ [W] ⋅ [v]

 

con [f] vettore riga e [v] vettore colonna e dove l’indice "r" di W è l’indice di riga (infatti se "r" varia lungo la riga di [f] allora il corrispondente indice di [W] varia lungo le colonne) e "s" è l’indice di colonna (infatti se "s" varia lungo la colonna [v] allora il corrispondente indice di [W] varia lungo le righe).

Considerando infine che si ha:

 

W(f,v) = f_r ⋅ v^s ⋅ W^r_s = f_r ⋅ T^r₀ ⋅ v^s ⋅ S⁰_s

 

e cioè, poiché T è un vettore e S è una forma lineare:

 

W(f,v) =f(T) ⋅ S(v)

 

si vede che è:

 

W = S⊗T

 

Come detto altrove, non tutti i tensori sono decomponibili, cioè risultano dalla moltiplicazione di due altri tensori.

 

▸    Prodotto interno (inner product) o composizione (composition) di due tensori

Combinando l’operazione di moltiplicazione di due tensori con quella di contrazione otteniamo l’operazione di inner product o composition:

 

 

Altrimenti detto, in modo più sintetico:

 

 

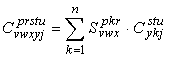
▸    Contrazione di un tensore

Consideriamo un tensore T^pqr_stu ed eguagliamo due degli indici, ottenendo: T^pkr_sku ; secondo vari autori, questo indicherebbe automaticamente una sommatoria rispetto agli indici. Se chiamiamo C il tensore contratto abbiamo:

 

C^pr_su = T^p1r_s1u + T^p2r_s3u + T^p3r_s3u + … + T^pnr_snu

 

ovvero, più sinteticamente:

 

 

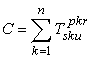
(questa è la definizione testuale di Levi-Civita)

Ovviamente, per ogni diverso valore di p, r, s, u, va fatta tale sommatoria, in modo che il tensore possiede tanti valori quante sono le combinazioni di tali indici, e quindi è complessivamente di ordine 4.

 

▸    Simmetrizzazione di un tensore

Un tensore è detto simmetrico in un paio di indici superiori o in un paio di indici inferiori se uno scambio degli indici non ne cambia il valore. Ad es., se il tensore T^rst_uvz è simmetrico rispetto agli indici s,t ciò vuol dire che si avrà:

 

S^r12_uvz = S^r21_uvz

 

per qualsiasi valore degli indici r,u,v,z

 

S^r13_uvz = S^r31_uvz

 

per qualsiasi valore degli indici r,u,v,z

 

S^r23_uvz = S^r32_uvz

 

per qualsiasi valore degli indici r,u,v,z (eccetera)

Se invece si ha:

 

S^r12_uvz = – S^r21_uvz

 

eccetera, allora il tensore è detto antisimmetrico

La simmetria e l’antisimmetria sono indipendenti dal sistema di coordinate scelto.

Dato un qualsiasi tensore di tipo (r,s), con r > 1 o s> 1, si può sempre costruire a partire da esso un tensore simmetrico e un tensore antisimmetrico rispetto a una qualsiasi coppia di apici o pedici. Per esempio, nel caso di un tensore di tipo (0,2) C_hj possiamo definire:

 

S_hj = ½ (C_hj + C_jh)

 

e

 

T_hj = ½ (C_hj – C_jk)

 

con S tensore simmetrico e T tensore antisimmetrico. Questo processo viene chiamato simmetrizzazione.

Un tensore può essere scritto come somma della cosiddetta parte simmetrica e parte antisimmetrica; nel nostro esempio si ha:

 

C_hj = ½ (C_hj + C_jk) + ½ (C_hj – C_jk)

 

Il processo di simmetrizzazione e di antisimmetrizzazione può essere generalizzato a una operazione avente ad oggetto più di due indici.

 

 

❍ Esempi di systems tensoriali

back to index

 

Ci sono molti tipi di systems tensoriali:

▸    Il tensore di stress, che possiede 18 componenti: 3 forze agenti su tre facce dell’elemento di volume (ciascuna è un vettore con 3 coordinate) e 3 deformazioni conseguenti a queste forze (ciascuna è un vettore con 3 coordinate)

▸Il tensore di inerzia

▸Il prodotto vettoriale

▸    Le coordinate vettoriali in uno spazio euclideo (tensore controvariante di ordine 1)

▸    La derivata ad una curva relativamente al parametro in un punto (tensore covariante di ordine uno)

▸    Il tensore metrico (tensore covariante di ordine due)

Esistono anche campi scalari, che tra i tutti i campi tensoriali hanno la peculiarità di non cambiare al cambiare delle coordinate.

 

 

❍ Tensori e manifolds: gli spazi tangenti

back to index

 

Il concetto di superficie come entità i cui punti sono dotati di posizione reciproca e coordinatizzazione mediante enople di Rⁿ è stato generalizzato dai matematici in quello di manifold (varietà )

Una varietà topologica n-dimensionale (manifold topologico n-dimensionale) è uno spazio topologico di Hausdorff X, che soddisfa al secondo assioma di numerabilità, e tale che ogni punto x ∈ X possiede un intorno aperto omeomorfo ad un aperto di Rⁿ.

Una superficie M (ad es. una calotta semisferica) immersa in uno spazio tridimensionale Rⁿ è un manifold bidimensionale, in quanto può essere coordinatizzata con due numeri. Una carta è una funzione u : M ➙ R² che assegna ad ogni punto della superficie una coppia di numeri reali.

Possiamo ottenere una semplice carta ruotando gli assi di R³ in modo che l’asse z sia parallelo al raggio verticale della semisfera ed assegnando ad ogni punto P di essa la coppia (a,b) che è la coordinata della proiezione di P sul piano xy:

 

 

Gli studiosi di algebra astratta compirono un importante lavoro di generalizzazione e di ridefinizione dei tensori. Essi notarono che ad ogni punto della superficie si può associare uno spazio tangente  che non è altro che lo spazio vettoriale delle tangenti o derivate direzionali vettoriali in quel punto.

Ogni tangente dello spazio è esprimibile come array di coordinate affini nella base data dalle derivate parziali rispetto ad x₁ e ad x₂.

Nella figura 0802101348 possiamo vedere il piano π tangente ad M nel punto P. I vettori appartenenti a tale piano tangente costituiscono uno spazio vettoriale bidimensionale, chiamato spazio vettoriale tangente. Nella figura sono mostrati due vettori che costituiscono una base privilegiata per tale spazio, il vettore ∂/∂x e il vettore ∂/∂y che rappresentano le derivate vettoriali della funzione u^–1 : R² ➙ M rispetto a v_x e v_y, versori nelle direzioni x e y.

Tali vettori ∂/∂x e ∂/∂y prendono il nome di coordinate vector fields; un qualsiasi vettore V può essere espresso nelle sue componenti nella base da essi rappresentata.

Gli algebristi misero in evidenza che al variare delle coordinate nello spazio dei parametri si verifica un cambio affine di coordinate nello spazio vettoriale e un corrispondente cambio del system tensoriale.

Ad ogni trasformazioni di coordinate:

 

                        x′ = x′ (x , y)

[0802101418]       …………......

                        y′ = y′ (x , y)

 

cambiano i coordinate vector fields e conseguentemente le coordinate di V espresse in termini della nuova base. La legge di trasformazione delle vecchie componenti (v¹,v²) di V nelle nuove componenti (v′¹,v′²) è legata a quella di trasformazione delle coordinate secondo la relazione:

 

 

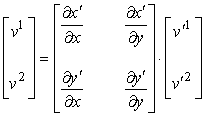
dove la matrice

 

 

è la matrice delle derivate parziali della trasformazione di coordinate nel punto P, detta anche matrice jacobiana.

Gli algebristi notarono che precisamente i systems tensoriali si modificano o secondo la legge di variazione di una forma multilineare sullo spazio tangente o secondo la legge di variazione di un funzionale multilineare al cambiare dei vettori che forniscono la base a tale spazio.

Una forma multilineare è una funzione

 

f : Tⁿ ➙ R

 

tale che si abbia:

 

f(k₁v₁,…,k_nv_n) = k₁f(v₁) + … + k_nf(v_n)

 

Quindi ogni tensore può essere visto come una forma multilineare del tipo

 

TxTx…xTxT*xT*x…xT* ➙ R

 

I simboli T* denotano lo spazio tangente duale, ossia lo spazio dei funzionali T ➙ R

Si parla anche di tensori di tipo (0,1) (tensore covariante di ordine uno) e di tensori di tipo (1,0) (tensore controvariante di ordine uno) e di tipo (1,1) (tensore misto, covariante di ordine uno e controvariante di ordine uno)

 

 

❍ La formalizzazione algebrica astratta dei tensori

back to index

 

Ma l’algebra astratta non si ferma qui, e generalizza ulteriormente il concetto di tensore.

Per spiegarlo consideriamo il caso di tensori covarianti di ordine due su uno spazio tangente T, e cioè tensori di tipo (0,1)

Questi tensori si modificano secondo la stessa legge in cui si modificano le forme bilineari su V, che portano due elementi di V in R. Le forme lineari costituiscono uno spazio a sé, diverso da V, e denotato con V* e chiamato spazio duale di V.

Indicheremo gli elementi di V* indifferentemente come tensori di tipo (0,1), tensori monocovarianti, forme lineari covarianti.

Il loro prodotto cartesiano è lo spazio V* x V*, che è da distinguersi dallo spazio dei tensori covarianti di ordine due.

Gli algebristi hanno notato che tutte le forme bilineari covarianti, cioè i tensori di tipo (0,2) su uno spazio vettoriale V di dimensione finita possono essere espressi come combinazioni lineari di prodotti tensoriali  di tensori (0,1) del tipo f⊗g dove il prodotto è dato da:

 

f⊗g(v,v’) = f(v) ⋅ g(v’)

 

Questo prodotto non è altro che l’ordinaria prodotto tensoriale esterno.

L’insieme delle forme bilineari covarianti, strutturata come spazio vettoriale con basi date dalle f⊗g, costituisce quello che viene chiamato prodotto tensoriale degli spazi duali V* e V*  e simboleggiato con V*⊗V* (si noti che ora abbiamo due accezioni di prodotto tensorlale : prodotto tra tensori e prodotto tra spazi vettoriali)

Esistono differenti tipi di spazi biprodotto, tra cui è possibile fare confusione; si tenga a mente che i tensori bicontrovarianti sono forme multilineari sullo spazio (VxV)* e non sullo spazio V*xV*; i tensori bicovarianti sono forme multilineari sullo spazio (V*xV*)* e non sullo spazio (VxV)**

Esistono elementi di V⊗V che non sono esprimibili nella forma v⊗w per due scalari v,w ∈ V. Si tratta dei tensori indecomponibili.

La esistenza di tensori indecomponibili mostra che la forma ⊗ : VxV ➙ V⊗V non è una bijezione, ma una semplice iniezione, e che l’insieme delle forme v⊗w = ⊗(v,w) genera V⊗V ma non lo esaurisce. Questo vuol altresì dire che non tutti i tensori possono essere rappresentati come moltiplicazione tensoriale di due tensori.

Tutto questo mostra infine che le classi di equivalenza entro lo spazio R^(VxV) delle funzioni VxV ➙ R aventi supporto finito non sono limitate alle classi corrispondenti ai vari v⊗w

Dire che non tutti i tensori di V⊗V non possono essere rappresentati nella forma.v⊗w non vuol dire invece che tutti i tensori di V⊗V non possano essere rappresentati nella forma

 

λ ⋅ v₁⊗v₂ + μ ⋅ v₃⊗v₄ +…

 

di combinazione lineare di tensori v_j⊗v_k ;  tutti i tensori possono essere comunque rappresentati (si veda altrove per questa dimostrazione) come combinazioni lineari nelle componenti della base biduale di V⊗V

Gli algebristi hanno notato che il prodotto V*⊗V* ha una proprietà molto peculiare, sintetizzata dal teorema sotto riportato:

 

Data una forma bilineare

 

h : V*xV* ➙ R

 

esiste una sola forma bilineare

 

b V*⊗V* ➙ R

 

tale che si abbia

 

h = b ∘ ⊗

 

 

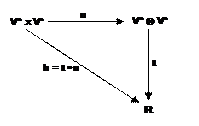
La forma

 

u : V*xV* ➙ R

 

è definita per ogni coppia (v,v’) dalla legge:

 

h(f,g) = f(v) ⋅ g(v’)

 

Consideriamo che scegliere un elemento (v,v’) ∈ V* x V* consiste nel fissare una forma dallo spazio dei tensori bicovarianti ad R, perché la

 

h(f,g) = f(v) ⋅ g(v’)

 

provvede a fornire una immagine ad ogni coppia (f.g) di forme lineari su V

Consideriamo che tale forma rende commutativo il diagramma:

 

h = b ∘ ⊗

 

Vediamo in tal modo che si può identificare V*⊗V* con lo spazio T_rs dei tensori di tipo (0,2) su V

 

Gli algebristi hanno poi generalizzato questa costruzione a spazi V₁xV₂ diversi di qualsiasi numero (inclusi spazi duali) e dimensione (inclusi quelli a dimensione infinita) e a forme bilineari verso uno spazio vettoriale qualsiasi (non necessariamente R) o addirittura un modulo su un anello.

Ne è risultata la nozione generale di prodotto vettoriale come oggetto algebrico astratto di cui il prodotto vettoriale V⊗V è solo un esempio particolare. La generalizzazione è data dal seguente teorema:

Per ogni modulo C sull’anello K e per ogni applicazione n-lineare

 

h : V₁ x … x V_n ➙ C

 

esiste una ed una sola applicazione lineare

 

t : V₁ ⊗ … ⊗ V_n ➙ C

 

che rende commutativo il diagramma:

 

 

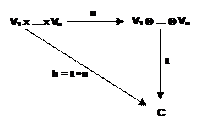
La teoria dei tensori ha così potuto essere riferita ad un oggetto algebrico lievemente meno generale, in cui gli spazi vettoriali V_n sono identici tra loro e in cui lo spazio immagine di h è lo spazio euclideo R, come mostrato dal diagramma sottostante, che ormai il lettore sa interpretare:

 

 

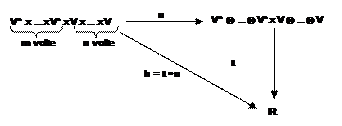
Gli elementi di V ⊗…⊗ V (r volte) si diranno tensori di tipo (r,0) ovvero tensori con r indici di controvarianza

Gli elementi di V* ⊗ V* (s volte) si diranno tensori di tipo (0,s) ovvero tensori con s indici di covarianza

Gli elementi di V* ⊗…⊗ V* ⊗ V ⊗…⊗ V (rispettivamente s ed r volte) si diranno tensori di tipo (r,s) ovvero tensori con r indici di controvarianza e s indici di covarianza.

 

 

 

❍ Approfondimenti di teoria algebrica astratta dei tensori

back to index

 

●  La base duale dello spazio V*

Consideriamo una qualsiasi funzione f ∈ V*; il suo valore per un qualsiasi vettore v ∈ V (che supponiamo di dimensione 2) sarà:

 

f(v) = f(λ₁ ⋅ b₁ + λ₂ ⋅ b₂)

 

e cioè

 

λ₁ ⋅ f(b₁) + λ₂ ⋅ f(b₂)

 

e cioè

 

f₁ ⋅ b₁*(v) + f₂ ⋅ b₂*(v)

 

dove f_i sono scalari e b_i* sono forme lineari che danno 1 se l’argomento è e_i, zero altrimenti. In virtù di questa definizione si ha infatti:

 

b_I*(v) = λ_i

 

Si vede quindi che ogni forma lineare può essere espressa come combinazione lineare delle b_i*, che pertanto sono basi di V*, dette anche basi duali, per la proprietà di assumere il valore 1 quando l’argomento è la corrispondente base di V.

 

●  La base duale dello spazio (VxV)*

Lo spazio (VxV)* è lo spazio delle forme bilineari (covarianti) su V².

Data una base {b_i}_i∈n con n dimensione di V, consideriamo il prodotto {b_i}_i∈n x {b_i}_i∈n costituito dalle coppie di basi del tipo:

 

(b_j,b_k)

 

Allora il valore di una funzione lineare F*(v,v’) sarà:

 

F*(b₁ ⋅ λ₁+…+ b_n ⋅ λ_n , b₁ ⋅ μ₁+…+ b_n ⋅ μ_n)

 

e cioè la sommatoria (usando la Einstein summation convention):

 

F*(b_j ⋅ λ_j , b_k ⋅ μ_k)

 

e cioè:

 

λ_j ⋅ μ_k ⋅ F*(b_j , b_k)

 

e cioè

 

λ_j ⋅ μ_k ⋅ ξ_jk ⋅ β_jk*(b_j , b_k)

 

dove

 

ξ_jk = F(b_j , b_k)

 

mentre β_jk* è una forma bilineare il cui valore è 1 se l’argomento è (b_j,b_k) e zero altrimenti. Sviluppando ancora, per la bilinearità di β_jk* si ha:

 

ξ_jk ⋅ β_jk*(b_j ⋅ λ_j  , b_k ⋅ μ_k)

 

e cioè

 

ξ_jk ⋅ β_jk*(v, v’)

 

da cui si vede che le β_jk* sono le basi duali dello spazio (VxV)*

Data la loro definizione si ha:

 

β_jk*(v,v’) = λ_j ⋅ μ_k

 

dove λ_j è il j-esimo coefficiente del vettore v di (v,v’) nella base {b} mentre μ_k è il k-esimo coefficiente del vettore v’ di (v,v’) nella base {b}

Espressa relativamente a queste basi una funzione b assume quindi la forma:

 

F = ξ₁₁ ⋅ β₁₁*+ … + ξ_nn ⋅ β_nn*

 

e cioè:

 

F(f,g) = (β₁₁* ⋅ ξ₁₁ + … + β_nn* ⋅ ξ_nn)(f,g) = ξ₁₁ ⋅ β₁₁*(f,g)+ … + ξ_nn ⋅ β_nn*(f,g)

 

Attenzione: esistono altre funzioni che danno 1 per un dato argomento, ma non sono bilineari. Le β_jk* sono invece funzioni bilineari.

 

●  La costruzione di V⊗W come insieme quoziente del modulo di funzioni

I moduli Rⁿ sono un caso particolare di moduli di funzioni R^X di tutte le funzioni X ➙ R

Se X è un qualsiasi insieme, il sottomodulo R^(X) del modulo di funzioni R^X che è generato dagli ε_x è un R-modulo libero sull’insieme {ε_x | x ∈ X}. Le forme ε_x(y) sono funzioni X ➙ R che hanno valore 1 se x = y, mentre hanno valore 0 altrimenti.

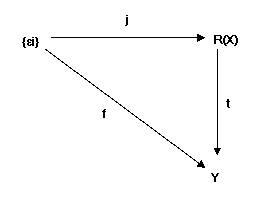
Il sottomodulo R^(X) può essere anche identificato con l’insieme di tutte le funzioni X ➙ R che hanno un supporto finito (il supporto di una funzione è l’insieme degli elementi del dominio con immagine non nulla).

 

 

Consideriamo il modulo di tutte le funzioni aventi supporto finito dal prodotto di due K-moduli A,B in K, che denomineremo K^(AxB)

Tale modulo F = K^(AxB) non è altro che il K-modulo generato dalle (a,b), ma può anche essere visto come l’insieme delle funzioni AxB ➙ K aventi supporto finito.

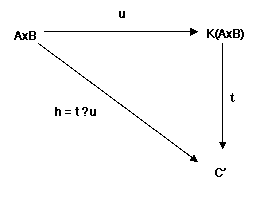
Se identifichiamo il K-modulo costituito dalle (a,b) con AxB allora la inserzione u : AxB ➙ K^(AxB) è universale per le funzioni dall’insieme AxB verso un K-modulo:

 

 

Ma u non è affatto bilineare; per es., se b ≠ 0 l’elemento (a₁,b) + (a₂,b) non è mai l’elemento (a₁ + a₂,b). Infatti, essendo u una iniezione, l’unico modo sarebbe che fosse 2b = b. Ma l’endomorfismo x ↦ b+x con b fisso è un automorfismo, e se fosse (b + b) + x = b + x sarebbe anche b + (b+x) = b+x da cui b = 0, che è contro l’ipotesi.

Per aggirare l’ostacolo consideriamo l’insieme quoziente composto dai laterali del sottomodulo S  generato da:

 

(a₁λ₁ + a₂λ₂ , b) – (a₁ , b) λ₁ – (a₂ , b) λ₂

(a , b₁λ₁ + b₂λ₂) – (a , b₁) λ₁ – (a , b₂) λ₂

 

per ogni scelta di λ_i , a, b rispettivamente appartenenti a K, A, B.

Denotato con a⊗b il laterale cui appartiene (a,b) si ha:

 

(a₁λ₁ + a₂λ₂) ⊗ b = (a₁ ⊗ b) λ₁ + (a₂ ⊗ b) λ₂

a ⊗ (b₁λ₁ + b₂λ₂) = (a ⊗ b₁) λ₁ + (a ⊗ b₂) λ₂

 

Questo perché ovviamente è:

 

(a₁λ₁ + a₂λ₂ , b)  = (a₁λ₁ + a₂λ₂ , b) – (a₁ , b) λ₁ – (a₂ , b) λ₂ + (a₁ , b) λ₁ + (a₂ , b) λ₂

 

il che vuol dire che

 

(a₁λ₁ + a₂λ₂ , b) + 0 = (a₁ , b) λ₁ + (a₂ , b) λ₂ + (a₁λ₁ + a₂λ₂ , b) – (a₁ , b) λ₁ – (a₂ , b) λ₂

 

e cioè (a₁λ₁ + a₂λ₂ , b) e (a₁ , b) λ₁ + (a₂ , b) λ₂ fanno parte dello stesso laterale.

Queste equazioni dicono che la funzione:

 

⊗ : A x B ➙ A ⊗ B

 

è bilineare e che il sottomodulo normale S è stato scelto abbastanza ampio da rendere bilineare il composto:

 

A x B ➙ F ➙ F/S

 

Questa funzione è universale:

 

 

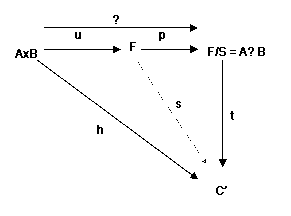
Per ciascuna funzione K-bilineare h : A x B ➙ C esiste una ed una sola trasformazione K-lineare t : A ⊗ B ➙ C’ tale che si abbia: h = ⊗ ∘ t