|
La formula di Taylor per funzioni
reali di variabile reale e per funzioni multivariate |
nozioni generali sulle funzioni
▸ La classificazione delle funzioni
▸ Le funzioni componenti di una
funzione Rn ➙
Rm
▸ Funzioni lineari e multilineari
definizione di
differenziabilità, differenziale, derivata, derivata parziale, derivata
direzionale
▸ (funzioni R ➙ R) Definizione di
differenziabilità, differenziale, derivata
teoremi sui rapporti tra
continuità e derivabilità
(funzioni r ➙ r) teoremi fondamentali
del calcolo
▸ (funzioni R ➙ R) Integrale indefinito
e teorema fondamentale del calcolo
▸ (funzione R ➙ R) Regola di De L’Hôpital
▸ (funzione R ➙
R) Teorema di Rolle
▸ (funzione R ➙ R) Teorema di Cauchy o
del valor medio
▸ (funzione R ➙ R) Teorema di Lagrange
nozioni generali sulla formula di
taylor
▸ Polinomio di Taylor e ordine
di contatto tra due funzioni
▸ Terminologia sulla formula di Taylor
(funzioni r ➙
r) formula di taylor
▸ (funzioni R ➙ R) Polinomio di Taylor
di ordine n
(funzioni r ➙ r) resto del polinomio
di taylor
▸ (funzioni R ➙
R) Il resto di Peano
▸ (funzioni R ➙ R) Il resto di Lagrange
▸ (funzioni R ➙ R) Altre forme di resto
della formula di Taylor. Il resto di Cauchy.
▸ (funzioni R ➙ R) Il resto integrale
(funzioni r ➙ r) dimostrazione della
formula di taylor
▸ (funzioni R ➙ R) La serie di Taylor
dimostrata da Courant
▸ (funzioni R ➙ R) La formula di Taylor
dimostrata da Citrini
(funzioni r ➙ r) formula di taylor calcolata mediante una
routine vba
▸ (funzioni R ➙ R) Formula di Taylor
calcolata mediante una routine VBA
(funzioni r ➙ r) teoremi sulla formula
di taylor
▸ (funzioni R ➙ R) Proprietà di
linearità del polinomio (operatore) di Taylor
▸ (funzioni R ➙ R) Proprietà di
sostituzione del polinomio (operatore) di Taylor
▸ (funzioni R ➙ R) Unicità del polinomio
di Taylor
(funzioni r ➙ r) formula di mac laurin
▸ (funzioni R ➙ R) Formula di Mac Laurin
(funzioni rn
➙ r)
Formula di taylor
▸ (funzioni Rn ➙ R) Derivata direzionale
iterata di ordine d di una funzione
▸ (funzioni Rn ➙ R) Esempio di
derivata iterata del terzo ordine di una funzione f : R3 ➙ R
▸ (funzioni Rn ➙ R) Polinomio di Taylor di
grado d di una funzione
(funzioni rn ➙
r) resto del polinomio di taylor
▸ (funzioni Rn ➙ R) Formula di
Taylor col resto di Peano
▸ (funzioni Rn ➙ R) Formula di
Taylor col resto di Lagrange
▸ (funzioni Rn ➙ R) resto integrale
▸ (funzioni Rn ➙ R) (resto
integrale) Espansione di Taylor con resto integrale per funzioni C∞
(funzioni r ➙ rn)
formula di taylor
▸ (funzioni R ➙ Rm) Formula di Taylor
(funzioni rn
➙ rm) formula di taylor
▸ (funzioni Rn ➙ Rm) Derivata
direzionale iterata di ordine d
▸ (funzioni Rn ➙
Rm) Polinomio di Taylor di ordine k
(funzioni di variabile complessa)
formula di taylor
nozioni generali sulle funzioni
▸ La classificazione delle funzioni
Le funzioni Rn ➙ Rm
tra spazi euclidei sono un sottogruppo delle funzioni tra spazi vettoriali di
dimensione qualsiasi.
Quando n = m = 1 una tale funzione è detta funzione a valori reali di una variabile reale.
Quando n = 1 e m > 1 è detta funzione
a valori vettoriali di una variabile reale
Quando n > 1 e m = 1 è detta funzione
a valori reali di variabile vettoriale, o semplicemente campo scalare
Quando n > 1 e m > 1 è detta funzione
a valori vettoriali di una variabile vettoriale, o semplicemente campo vettoriale
Per evitare ingombranti denominazioni, nel prosieguo
parleremo rispettivamente di funzioni R ➙ R, funzioni
R ➙ Rm,
funzioni Rn ➙
R e funzioni Rn ➙
Rm anche se tecnicamente esse potrebbero essere definite solo su un
sottoinsieme dello spazio euclideo indicato come dominio.
Molti autori
seguono la regola che se il simbolo di funzione non è in grassetto e
l’argomento è in grassetto si tratta di una funzione Rm ➙ R, mentre, se anche il simbolo di funzione è in grassetto
si tratta di una funzione Rm ➙
Rn
▸ Le funzioni componenti di una
funzione Rn ➙ Rm
Data una funzione f : Rn ➙ Rm,
essa può essere rappresentata come una m-pla di funzioni
componenti fi : Rn ➙ R:
y1 = f1(x1,
…, xn)
………………….
ym = fm(x1,
…, xn)
in modo che si abbia:
f(x1,…,xn) = (f1(x1,…,xn),
…, fm(x1, …, xn))
I rapporti tra le funzioni componenti ed f sono molto
importanti:
▸ La funzione f è continua se e solo se le
funzioni componenti sono continue
▸ La derivata della funzione f nella direzione
del vettore v è costituita dalla enopla delle derivate delle funzioni
componenti:
Dvf = (Dvf1, …, Dvfm)
▸ Funzioni lineari e multilineari
Una funzione f : Rn ➙ Rm
è una funzione lineare se si ha:
f(a ⋅ v
+ b ⋅
w) = a ⋅ f(v) + b ⋅ f(w)
dove v,w ∈ Rn e a,b ∈ R
La linearità non è da confondere con la multilinearità. Una funzione multilineare è una funzione g : Rn
x … x Rn che manda k vettori di Rn in Rm e
tale che la funzione è lineare rispetto ad ogni vettore della k-pla:
g(u, v, a ⋅ w1 + b ⋅ w2, x, y)
= a ⋅ g(u, v, w1, x, y) + b ⋅ g(u, v, w2, x, y)
Una funzione f : Rn ➙ Rm
è lineare se e solo se esistono numeri aij, i = 1,…,m, j = 1,…,n,
tali che le funzioni componenti f1,…,fm di f sono date
da:
f1(x) = a11x1
+ a12x2 + … + a1nxn
f2(x) = a21x1
+ a22x2 + … + a2nxn
……………………………………
fm(x) = am1x1
+ am2x2 + … + amnxn
La funzione f è determinata completamente dalla matrice A =
(aij) e può scriversi sotto forma di moltiplicazione matriciale:
f(v) = A ∘
v
e cioè:

definizione di
differenziabilità, differenziale, derivata, derivata parziale, derivata
direzionale
▸ (funzioni R ➙ R) Definizione di differenziabilità,
differenziale, derivata
Una funzione f è una funzione
derivabile in un punto x0 se si può scrivere:
f(x0 + ∆x) – f(x0) = f′(x0)
⋅ ∆x + o(∆x)
(∆x ➙ 0)
dove per o(∆x) (notazione di Landau) si intende
una funzione α tale che ![]()
In altre parole,
trascurando gli infinitesimi superiori al primo, l’incremento di f è dato dalla funzione lineare in ∆x:
φ(∆x) = f′(x0) ⋅ ∆x
La funzione
lineare che approssima l’incremento
∆x è chiamata differenziale della
funzione f in x0.
Equivalentemente, la funzione f è differenziabile in x0 se si ha:
![]()
▸ (funzioni Rn ➙ R) Definizione di differenziabilità,
differenziale, derivata direzionale, derivata parziale
Sia f : A ⊆ Rn ➙
R una funzione definita su un aperto A di R e sia x0 interno ad A.
Si dice che f è una funzione differenziabile in x0 se
esiste una funzione lineare L : Rn ➙ R per cui si
abbia:
f(x0 + ∆x) – f(x0) = L(∆x) + o(∥∆x∥)
dove una funzione φ è detta essere o(∥∆x∥) se è: ![]()
Per funzione
lineare si intende una funzione f : Rn ➙ R tale che, dati gli scalari ai e i vettori vi
si abbia:
f(v1, …, ai ⋅ vi + bi ⋅ wi, …, vn) = ai ⋅ f(v1, …,vi, …, vn) + bi ⋅ f(v1,…, wi, …, vn)
La funzione L è
definita univocamente dalla condizione di differenziabilità e prende il nome di
differenziale di f in un punto x0
ed è anche simboleggiata con dfx0, mentre il simbolo Dfv(x0),
viene normalmente riservato alla derivata direzionale (vedi più avanti).
A volte L viene
detta differenziale totale per distinguerla
dai differenziali parziali dx1f, …, dxnf, che sono le
derivate parziali, meglio indicate con ∂f/∂xi,
Dxif, fxi.
La funzione L è
detta parte principale dell’incremento ∆f = f(x0 + ∆x) – f(x0)
e la funzione φ si dice essere un infinitesimo di ordine superiore (al primo)
rispetto a ∥∆x∥.
In trattazioni più avanzate il differenziale è definito come
una funzione
dallo spazio tangente di un punto x0 del dominio allo spazio
tangente del punto f(x0) del codominio.
Alcuni autori
distinguono il "differenziale della funzione
in un punto x0" dal "differenziale
della funzione f" senza altre specificazioni, che è la funzione Rn
➙ L(Rn ➙ R) che per ogni punto p di Rn fornisce il differenziale dfx0,
dove L(Rn ➙ R) è lo spazio vettoriale delle funzioni lineari Rn
➙ R.
Equivalentemente, una funzione f è differenziabile
se esiste una funzione lineare L tale che si ha:
![]()
Equivalentemente, una funzione f è differenziabile
se esistono le derivate parziali i-esime, date da:
![]()
ed esiste una
funzione lineare di tali derivate parziali (talvolta simboleggiata con ∇f ⋅ ∆x) tale che sia:
![]()
dove è ![]()
Equivalentemente, una funzione f è differenziabile
se esiste una matrice mxn (nel caso Rn ➙ R la matrice è una matrice-riga di dimensione 1xn) tale
che sia:
![]()
dove "∘" è una moltiplicazione
matriciale e dove è ![]()
Tale matrice è
chiamata da taluni derivative.
Equivalentemente, vengono dapprima definite le
derivate parziali, date da:
![]()
se le derivate
parziali esistono e sono continue, allora l’espressione ![]() costituisce la parte principale dell’incremento
totale della funzione e si definisce differenziale totale e differisce da ∆f di un infinitesimo di ordine superiore rispetto a ∥∆x∥.
costituisce la parte principale dell’incremento
totale della funzione e si definisce differenziale totale e differisce da ∆f di un infinitesimo di ordine superiore rispetto a ∥∆x∥.
Se consideriamo
Df(x0)(v) come una funzione che fornisce la derivata direzionale
nella direzione di un vettore v, troviamo che non sempre è una mappa lineare:
questo avviene solo se f è una funzione differenziabile; allora la funzione che
fornisce la derivata ha la forma di un differenziale df(x0), cioè di
una mappa lineare che approssima la funzione f(x) – f(x0). Nel caso di non-differenziabilità,
invece, esiste la mappa Df(x0) che fornisce la derivata, mentre non
esiste il differenziale df(x0)
Al differenziale
df si contrappone l’incremento ∆f della funzione; per valori infinitesimi di ∆x si ha df ≃ ∆f.
Data una funzione f : Rn ➙ Rm, la funzione che associa ad ogni punto p ∈ Rn la funzione lineare
dfp : Rn ➙
R è una forma differenziale (lineare).
Una forma differenziale lineare
su Rn è un polinomio omogeneo di primo grado nelle componenti di un
vettore dx:
![]()
che varia da punto a punto. Considerando dx come argomento,
tale polinomio rappresenta in ogni punto una funzione lineare Rn ➙
R. Una forma lineare può essere identificata con le n funzioni continue che in
ogni punto forniscono i valori ak.
Non tutte le forme differenziali lineari sono forme
differenziali di una funzione. Se, data una forma differenziale lineare
definita in un aperto A ⊆
Rn esiste una funzione f di classe C1 le cui derivate
parziali k-esime forniscono il k-esimo coefficiente ak della forma,
allora si dice che la funzione f è una primitiva o un potenziale della forma, e
la forma stessa si dice esatta.
Chiamiamo
ogni vettore unitario v ∈ Rn una direzione in Rn. La derivata direzionale di f in x0 nella
direzione v è il limite:
![]()
Alcuni autori considerano un vettore v qualsiasi (anche non
unitario) e chiamano derivata direzionale nella direzione di v il limite
ottenuto considerando tale vettore.
Le n derivate
parziali di f non sono altro che le derivate direzionali rispetto alle basi
standard di Rn:
e1 =
(1, 0, …, 0)
e2 =
(0,1,0, …, 0)
………………….
en =
(0, …, 0, 1)
le basi standard di Rn
sono quelle che esprimono un vettore con coefficienti che coincidono con le
componenti del vettore:
v = (v1, …, vn) = e1 ⋅ v1
+ e2 ⋅ v2 + … + en ⋅ vn.
Le derivate parziali sono date dal limite: ![]() .
.
Si vede come si tratti della derivata della funzione R ➙
R ottenuta facendo variare la variabile xi e tenendo le rimanenti
variabili x1, …, xi–1, xi+1, …, xm
fisse.
Esse verranno
indicate con ![]() o anche con Dif(a) = Deif(a):
o anche con Dif(a) = Deif(a):
Se la funzione f è differenziabile, allora le derivate
parziali e in genere le derivate direzionali sono date dal differenziale:
Dvf(a) = dfa(v) = L(v)
Come già detto sopra, il fatto che una funzione abbia tutte
le derivate direzionali in un punto non implica che sia derivabile in tale
punto, se Dvf(a) ≠
L(v) allora la funzione Dv(x0) non è una funzione lineare
e f non è differenziabile.
Ad es. la
funzione ![]() ha tutte le derivate direzionali
nel punto x0 = (0,0), ma la funzione Dv(x0)
non è una funzione lineare, e quindi l’immagine di R2 nella funzione L non forma un
piano tangente il punto a.
ha tutte le derivate direzionali
nel punto x0 = (0,0), ma la funzione Dv(x0)
non è una funzione lineare, e quindi l’immagine di R2 nella funzione L non forma un
piano tangente il punto a.
Se la funzione f è differenziabile, allora le derivate
direzionali sono una combinazione lineare delle derivate parziali:
![]()
▸ (funzioni Rn ➙ Rm) Definizione di
differenziabilità, differenziale, derivata direzionale, derivata parziale
Se esiste una trasformazione lineare L : Rn ➙
Rm tale che
[0812181947] ![]()
allora diciamo che f è una funzione
differenziabile in b.
Equivalentemente, una funzione f è una
funzione differenziabile se esiste una applicazione lineare L : Rn ➙
Rm tale che si abbia:
[0812181948] f(x0 + h) – f(x0)
= L(h) + o(∥h∥) per h ➙
0
La formula [0812181948] è l’equivalente della formula [0812181947], perché la funzione
o(∥h∥) è precisamente la funzione f(x) – f(x0) – L(x –
x0), che, come si vede, ha limite zero rispetto ad ∥h∥ per h ➙
0
L’applicazione L, univocamente
determinata dalle condizioni [0812181947] o [0812181948] viene chiamata il differenziale della funzione f in
x0. Si scrive anche L = f′(x0).
Nella formula [0812181947] il limite zero non è uno scalare
ma un vettore, perché la quantità rappresentata dalla frazione è un vettore
appartenente al codominio di f. Che è lo stesso che dire che il limite φ(h)/ ∥h∥
relativo alla funzione φ(h)
= o(∥h∥)
nella formula [0812181948],
anche se il denominatore è scalare, è un limite vettoriale.
Alcuni autori
distinguono il "differenziale della funzione in un punto x0"
dal "differenziale della funzione f" senza altre specificazioni, che
è la funzione Rn ➙
L(Rn ➙ Rm) che per ogni punto
p di Rn
fornisce il differenziale dfx0, dove L(Rn ➙ Rm) è lo spazio
vettoriale delle funzioni lineari Rn ➙ Rm.
Equivalentemente, data una funzione f : Rn ➙ Rm, esiste una funzione
lineare Dx0f : Rn ➙ Rm tale che per ogni intorno N della mappa
lineare zero in L(Rn ; Rm), c’è un intorno N′ di zero ∈
Rn tale che se t ∈
N′ allora
f(x+t) – f(x) = Dx0f(t) + A(t)
per qualche A ∈ N.
Equivalentemente, la funzione f : Rn
➙
Rm è differenziabile in a sse ognuna delle sue funzioni componenti f1,
…, fn è differenziabile. In tal caso il differenziale di f è dato
da:
dfa = (dfa1, …, dfan)
La derivata direzionale
di f in x0 nella direzione del vettore v è il vettore:
![]()
In pratica si tratta del vettore velocità γv′(0) : della curva
γv
: R ➙
Rm : h ↦ f(x0 + h ⋅ v)
con γv(0) = x0
La derivata direzionale nella direzione di un versore base è
chiamata la derivata parziale di f rispetto
al k-esimo componente di x.
La matrice mxn della funzione lineare L nelle basi standard
di Rn ed Rm coincide con la matrice
jacobiana delle derivate parziali, cioè la sua i-esima riga, j-esima
colonna è la derivata parziale j-esima della funzione componente i-esima:
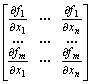
dove le fi sono le n funzioni componenti Rn
➙
R tali che f(x1,…,xn) = (f1(x1,…,xn),
…, fm(x1, …, xn))
Da alcuni autori tale matrice mxn di L viene chiamata la
derivata della funzione nel punto x0 simboleggiata da f′(x0).
Possiamo pertanto dire equivalentemente che la
funzione f : Rn ➙ Rm
è differenziabile se esiste una matrice J di dimensione mxn tale che sia:
[0812191937] f(x0 + h) – f(x0)
= J ∘ h + φ(h)
dove “∘”
è la moltiplicazione matriciale e limh➙ 0 φ(h)/∥h∥ = 0
Si può dimostrare che se la funzione f è differenziabile,
allora le derivate parziali e in genere le derivate direzionali sono date dal
differenziale:
Dvf(a) = dfa(v)
Quindi, se una funzione è differenziabile, le derivate
direzionali si ottengono applicando la matrice jacobiana al vettore di Rn
rispetto a cui è calcolata la derivata direzionale:
Dvf(a) = J ⋅ v
dove la moltiplicazione è il prodotto matriciale:
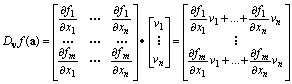
Essendo tale matrice, come detto, formata dalle derivate
parziali, si vede, dalla formula matriciale sopra indicata, che le derivate
direzionali nella direzione del vettore v = (v1,…,vn)
sono esprimibili come combinazione lineare delle derivate parziali moltiplicate
per le componenti vi:
Dvf(a) = ∑1≤j≤nvjDjf(a)
Possiamo dire equivalentemente
che una funzione f : Rn ➙ Rm è differenziabile se esistono le derivate
parziali ed esiste una funzione lineare con coefficienti dati dalle derivate
parziali che approssima f(x0 + h) – f(x0) a meno di infinitesimi superiori al primo
per h ➙ 0.
Possiamo dire equivalentemente
che una funzione f : Rn ➙ Rm è differenziabile se e solo se esistono e
sono continue le derivate parziali delle funzioni componenti, perché in tal
caso esiste una mappa
lineare L : Rn ➙
Rm tale che:
f(a + h) = f(a) – L(h) + R(h)
con limh➙0
R(h)/|h| = 0
(si noti che 0 è un vettore)
Tale mappa
lineare può essere visualizzata come:
f(h) = ![]()
dove il vettore ![]() approssima
f(x + h) – f(x) a meno di infinitesimi superiori al primo per h ➙
0.
approssima
f(x + h) – f(x) a meno di infinitesimi superiori al primo per h ➙
0.
Sia f : U ⊂ E ➙ F una funzione
tra spazi vettoriali dotati di norma, dove U è un aperto in E. Diciamo che f è una funzione differenziabile in un punto x0
se esiste una funzione lineare L : E ➙ F tale che sia:
![]()
dove ∥⋅∥ rappresenta la norma
nello spazio appropriato.
La mappa L viene detta il differenziale
di f nel punto x0.
La mappa
Df : U ➙ L(E,F) : u ↦ Df(u)
(dove L(E,F) è lo
spazio delle funzioni lineari tra E ed F) è il differenziale di f.
Data una funzione f : X ➙ X' tra spazi
affini, una derivata di f in x0 ∈ X è una funzione lineare Dx0f : Tx0X
➙ Tf(x0)X' tra gli spazi
tangenti rispettivamente ad x0 e ad f(x0), tale che per
ogni intorno della mappa lineare nulla in L(Tx0X ; Tf(x0))
c’è un intorno N' di 0 ∈ Tx0X tale che se t ∈ N' allora
d'(f(x+t),f(x)) =
d'f(x0)(Dx0f(t) + A(t))
per qualche A ∈ N.
Dove d' : X'xX' ➙ T è una funzione che porta una
coppia di vettori di un insieme X in un vettore dello spazio vettoriale T
associato allo spazio affine.
teoremi sui
rapporti tra continuità e derivabilità
▸
(funzioni Rn
➙ R) Se una funzione è
differenziabile in un punto è ivi continua
▸ (funzioni Rn ➙ R) Se una funzione possiede derivate
parziali continue nell’intorno di un punto, è ivi differenziabile.
▸
(funzioni Rn ➙ R) La
differenziabilità in un punto implica l’esistenza di tutte le derivate
direzionali, ma non è vero in generale l’inverso.
▸
(funzioni R ➙ R) Se una
funzione ha una derivata in un punto allora è continua in quel punto
(funzioni Rn
➙
Rm) Non è sempre vero che una funzione che ha una derivata in un
punto è continua in quel punto.
(funzioni r ➙ r) teoremi fondamentali del calcolo
▸ (funzioni R ➙ R) Integrale indefinito e teorema
fondamentale del calcolo
Una funzione A(x) è un integrale indefinito della funzione
f(x) se quest’ultima ne costituisce la derivata. Abbiamo allora:
![]()
cioè (teorema fondamentale del calcolo) l’operazione di
integrazione è l’inversa di quella di derivazione: integrando la derivata di
A(x) si ottiene A(x)
▸ (funzione
R ➙ R) Regola di De L’Hôpital
Siano date due funzioni f(x) e g(x) e si supponga che
▸ Il
quoziente f(x) / g(x) assuma in un punto x0 ∈
ℝ̅ la
forma indeterminata
▸ f(x)
e g(x) siano continue e derivabili in un intorno (destro, sinistro, bilatero) U0
di x0, x0 escluso
▸ Sia
g′(x) ≠ 0 per x ≠
x0
▸ Esista,
finito o infinito, il limite (destro, sinistro, bilatero):
![]()
Allora esiste anche il limite per x ➙ x0
di f(x)/g(x) e coincide con ℓ
▸ (funzione
R ➙ R) Teorema di Rolle
Se una funzione f ∈ C0([a,b]) assume valori uguali agli estremi
dell’intervallo [a,b] ed è derivabile in
tutti i punti interni a tale intervallo, esiste almeno un punto ξ
∈ (a,b) in cui f′(ξ) = 0
▸ (funzione R ➙ R) Teorema di Cauchy o del valor medio
Siano date due funzioni, f,g continue in un intervallo
chiuso [a,b] e derivabili in (a,b). Allora esiste almeno un punto ξ ∈ (a,b) in cui:
g′(ξ) [f(b) – f(a)] = f′(ξ) [g(b) – g(a)]
Se si suppone inoltre che la derivata g′(x) non si annulli in tutto (a,b),
risulta necessariamente g(b) ≠ g(a) (per il teorema di Rolle), e
la relazione precedente si scrive:
![]()
▸ (funzione
R ➙ R) Teorema di Lagrange
Data una funzione f ∈ C0([a,b]) e derivabile in (a,b) esiste almeno
un punto ξ ∈ (a,b) in cui:
![]()
o, equivalentemente:
f(b) = f(a) + f′(ξ)
(b - a)
nozioni generali sulla formula di
taylor
▸ Polinomio di Taylor e ordine di
contatto tra due funzioni
▸ Si
dice che due funzioni f e g hanno contatto di
ordine n in x0 se la loro differenza è infinitesima di ordine
superiore ad n in x0
▸ Una
funzione f e il suo polinomio di
Il polinomio di Taylor è l’unico ad avere tale contatto. Per
questa caratteristica si chiama anche polinomio osculatore di ordine n di f in
x0
▸ Terminologia sulla formula di Taylor
▸ Una
espansione di Taylor che, a parte il resto,
Poiché, data una
funzione f, esiste un solo polinomio di grado ≤ n le cui derivate in x0 coincidono fino alla n-esima
con quelle di f, il polinomio di Taylor dipende da n, f, x0, x,
pertanto
viene indicato in vari modi:
Pn(f,x,x0)
Pnf(x,x0)
Pn(x,x0)
Pn(x)
Noi utilizzeremo
più frequentemente quest’ultimo
simbolo
La funzione f(x) – Pn(x) si denomina resto n-esimo del polinomio di Taylor e viene
indicata in vari modi:
Rn(x,x0)
Rn(x)
dei quali noi
utilizzeremo l’ultimo.
Taluni autori
considerano il polinomio e il resto non funzioni di x, ma di h = x – x0 e scrivono:
Pn(x – x0)
Rn(x – x0)
Rn(x,x0) è infinitesimo di ordine
superiore a (x – x0)n
▸ L’operatore di Taylor di grado n è l’operatore T della formula:
Pn(x,x0) = Tn(f)
Perciò il simbolo Tn(f) può essere utilizzato
intercambiabilmente con quello del polinomio di Taylor
▸ Attenzione:
serie di
▸ Si
trova in certi autori anche l’espressione
espansione di
(funzioni r ➙ r) formula di taylor
▸ (funzioni R ➙ R) Polinomio di Taylor di ordine n
▸ La formula del polinomio di Taylor di ordine n
per una funzione f : R ➙ R è la
seguente:
![]()
dove f(k)(x0) è la derivata k-esima
nel punto x0.
In pratica, il termine ![]() , derivato k volte dà 1, mentre derivato un
numero inferiore o un numero superiore di volte dà zero. Pertanto il polinomio
di Taylor Pn(x – x0) ha le derivate successive alla
n-esima identicamente eguali a zero.
, derivato k volte dà 1, mentre derivato un
numero inferiore o un numero superiore di volte dà zero. Pertanto il polinomio
di Taylor Pn(x – x0) ha le derivate successive alla
n-esima identicamente eguali a zero.
Aggiungiamo ora al polinomio di Taylor il resto, cioè una
funzione Rn(x) = f(x) – Pn(x,x0):
[0812112004] ![]()
Per la
costruzione del polinomio di Taylor si ha:
[0812201905] ![]()
Se esiste la
derivata n-esima in x0, sarà dimostrato più avanti che è:
[0812112007] ![]()
e cioè:
[0812112008] ![]() (resto di Peano)
(resto di Peano)
▸ Se
invece, oltre alla derivata n-esima, supponiamo che la derivata (n +1)-esima
esista nell’intervallo aperto (x0,x), possiamo garantire l’esistenza
di almeno un punto ξ ∈ h in cui risulti:
[0506281102] ![]()
e cioè:
[0506281103] ![]() (resto
di Lagrange)
(resto
di Lagrange)
(funzioni r ➙ r) resto del polinomio di taylor
▸ (funzioni
R ➙ R) Il resto di Peano
Supponiamo che la funzione f sia dotata di derivate fino
alla (n + 1)-esima nel solo punto x0. Possiamo allora applicare
ripetutamente la regola di De L’Hopital al rapporto
![]()
ottenendo, dopo n passaggi:
[0812061925] ![]()
Notiamo che é:
Rn(n)(x0) = 0
Infatti, per la costruzione del polinomio di Taylor, questo
ha le stesse derivate fino all’ordine n, e si può scrivere:
Dn(x0)[ Tn + Rn
] = f(n)(x0)
da cui:
f(n)(x0) + Rn(n)(x0)
= f(n)(x0)
da cui si vede che la derivata n-esima del resto n-esimo è
zero. Questo fa sì che possiamo sommare Rn(n)(x0)
in qualsiasi punto della [0812061925] e
quindi scrivere:
[0812061926] ![]()
Poiché è Rn(n+1)(x0) = f(n+1)(x0)
ed è:
[0812061935] ![]()
possiamo scrivere:
[0812061932] ![]()
da cui, sostituendo la [0812061932] nella [0812061925]
otteniamo:
[0812061934] ![]()
da cui, per le proprietà dei limiti, possiamo scrivere:
[0812061936] ![]()
e cioè:
[0812061938] ![]()
e cioè:
[0702260738] ![]()
che è il resto di Peano nella sua prima forma.
Se scriviamo la [0702260738] come:
[0702260739] ![]()
notiamo che il primo addendo non è altro che il termine (n +
1)-esimo dello sviluppo di Taylor, togliendo il quale abbiamo il resto del
polinomio di ordine (n + 1):
[0702260740] ![]()
Applicando passaggi analoghi al polinomio di Taylor e al
resto di ordine (n – 1), e scrivendo
o(x – x0) = α(x)
otteniamo facilmente:
[0702260741] ![]()
e poiché α(x)
è infinitesima per x ➙
x0 abbiamo:
[0702260742] ![]()
e quindi possiamo riscrivere la [0702260741] come:
[0702260743] ![]()
che è il resto di Peano nella seconda forma, che richiede
solo che la funzione sia derivabile n volte in x0 e non l’esistenza
della f(n+1)(x0).
La condizione che f sia derivabile n volte implica che f(n–1)
esista in tutto un intorno di x0.
▸ (funzioni
R ➙ R) Il resto di Lagrange
▸ Il resto di Lagrange
Si supponga che esista la (k +1)-esima derivata della
funzione f : R ➙
R in ciascun punto dell’intervallo chiuso I con punto iniziale x0 e
punto finale x. Allora esiste un punto x0 ≤ Ϛ ≤
x tale che
![]()
Questa formula è conosciuta come resto di Lagrange.
Se, in aggiunta, si ha |f(k+1)(σ)| ≤ M per ogni Ϛ ∈
I allora è:
![]()
e inoltre:
![]()
in particolare tale formula vale se f(k+1) è
continua nel punto x0, perché allora sarà necessariamente limitata
da un qualche valore M su un intervallo aperto contenente x0.
▸ Dimostrazione
del resto di Lagrange
Invece di supporre che esista f(n+1) in x0
(ipotesi da cui si ricava il resto di Peano) facciamo l’ipotesi che la derivata
di ordine n + 1 esista nell’intervallo aperto (x0,x) (dunque non
necessariamente in x0).
Dal teorema di Cauchy si deduce che, date f,g continue in un
intervallo chiuso [a,b] e derivabili nell’intervallo aperto (a,b), se la
derivata g′(x) non si annulla in tutto (a,b),
esiste un punto ξ ∈ (a,b) in cui è:
[0702260738] ![]()
Tenuto conto che è:
[0703042029] ![]()
dato che i secondi addendi del numeratore e denominatore
valgono zero, possiamo applicare ripetutamente la [0702260738] al secondo
rapporto della [0703042029] ottenendo:
[0702260739] ![]()
Scriviamo il secondo rapporto della [0702260739] come:
[0703042033] ![]()
Il
teorema di Lagrange dice che data una funzione f ∈ C0([a,b]) e derivabile in (a,b) esiste almeno
un punto ξ ∈ (a,b) in cui:
![]()
Applicando il teorema di Lagrange alla [0703042033]
possiamo garantire l’esistenza di almeno un punto ξ ∈ (x0,x) in cui risulti:
[0703042035] ![]()
Poiché è:
[0703042037] ![]()
possiamo scrivere:
[0703042039] ![]()
e quindi, per la [0702260739]:
[0703042041] ![]()
e cioè il resto della formula di Taylor nella forma di
Lagrange:
[0703042043] ![]()
▸ (funzioni R ➙ R) Altre forme di resto della formula
di Taylor. Il resto di Cauchy.
Supponiamo che f(n+1) esista in un intervallo
aperto (h,k) contenente x0 e che f(n) sia continua
nell’intervallo chiuso [h,k]. Scegliamo un x ≠ x0 in [h,k]. Per fissare le idee supponiamo che
sia x > a. Manteniamo x fisso e definiamo una nuova funzione F sull’intervallo [a,x] come segue:
[0812070529] ![]()
Si osservi che F(x) = f(x) e F(x0) = Tnf(x;x0),
e dunque F(x) – F(a) = Rn(x). La funzione F è continua
nell’intervallo chiuso [x0,x] e derivabile nell’intervallo aperto (x0,x).
Se calcoliamo F′(t)
tenendo presente che ognuno dei termini della somma che definisce F(t) è un
prodotto, troviamo che tutti i termini si semplificano eccetto uno, e siamo
condotti all’equazione:
[0812070538] ![]()
Sia ora G una qualsiasi funzione continua su [a,x] e
derivabile su (a,x). Ad essa possiamo applicare il teorema di Cauchy e
scrivere:
[0812070530] ![]()
per qualche c nell’intervallo aperto (x0,x). Se G′ non si annulla in (x0,x)
ciò ci fornisce la seguente espressione per il resto:
[0812070543] ![]()
Possiamo esprimere l’errore in molte forme, con differenti
scelte di G. Prendendo ad es. G(t) = (x – t)n+1 otteniamo la forma
di Lagrange:
[0812070546] ![]()
Prendendo G(t) = x – t otteniamo un’altra formula, detta
forma di Cauchy del resto:
[0812070549] ![]()
Se G(t) = (x – t)p, con p ≥ 1, otteniamo la formula
[0812070551] ![]()
▸ (funzioni R ➙ R) Se f(n+1) esiste allora
la derivata (n+1)-esima del resto del polinomio di Taylor di grado n non è
altro che f(n+1)
In pratica, il termine ![]() , derivato k volte dà 1, mentre derivato un
numero inferiore o un numero superiore di volte dà zero.
, derivato k volte dà 1, mentre derivato un
numero inferiore o un numero superiore di volte dà zero.
Pertanto il polinomio di Taylor Pn(x – x0)
ha le derivate successive alla n-esima identicamente eguali a zero.
Questo implica altresì che se esiste la derivata f(n+1)
allora è:
Rn(n+1) = f(n+1)
perché per ipotesi il polinomio di Taylor di grado n ha
nulle le derivate superiori alla n-esima.
▸ (funzioni
R ➙ R) Il resto integrale
Se f ∈ Cn+1 in un intervallo
contenente x0 si ha: ![]() col resto
col resto ![]()
▸ (funzioni R ➙ R) Se la derivata f(n) è
continua in x0 allora il resto è un infinitesimo di ordine superiore
rispetto ad (x – x0)
Se la derivata f(n)
è continua in x0 si ha ![]()
▸ Dimostrazione
che è ![]()
Infatti è:
f(x) = Pn - Rn
ma anche
f(x0) = P(x0)
per cui
![]()
▸ Dimostrazione
che è ![]()
Infatti si ha:
![]()
![]()
![]()
![]()
![]()
▸ Dimostrazione
che è ![]()
Supponiamo che f sia derivabile in tutto un intorno di x0.
Applicando la regola di de L’Hopital si ha:
![]()
ammesso che quest’ultimo limite esista. Quindi, se f ammette
derivata seconda in x0 si ha:
![]()
da cui si ricava che:
![]()
Isolando il termine f(x) al primo membro si ottiene:
![]()
▸ Iterando
il numero desiderato di volte lo stesso procedimento utilizzato per dimostrare
che è ![]() si
ottiene infine che, se esiste f(n)(x0) è:
si
ottiene infine che, se esiste f(n)(x0) è: ![]()
▸ (funzioni R ➙ R) Per la sua costruzione, il resto
della formula di Taylor di grado n si annulla in x0 assieme a tutte
le sue derivate fino al grado n incluso.
(funzioni r ➙ r) dimostrazione della formula di taylor
▸ (funzioni R ➙ R) La serie di Taylor dimostrata da
Courant
Invece di una
dimostrazione rigorosa della formula di Taylor, partiremo dai seguenti
presupposti:
▸ Che
sia possibile esprimere funzioni
(1) f(x)
= c0 + c1x + c2x2 + …
mediante una legge che esprima i coefficienti ci
per mezzo della funzione f e delle sue derivate
▸ Che
f(x) sia indefinitamente derivabile nel punto x0
▸ Che
una serie di potenze possa essere derivata termine a termine
In queste ipotesi, si possono determinare i coefficienti cn
dalla conoscenza del comportamento di f(x) nell’intorno di x = 0.
Sostituendo x = 0 nella (1) si ottiene:
c0 = f(0)
Derivando la (1) si ottiene poi:
(2) f′(x) = c1 + 2c2x
+ 3c3x2 + …
Sostituendo di
nuovo x = 0 si ottiene:
c1 = f′(0)
derivando la (2)
si ottiene:
(3) f″(x) = 2c2 + 2‧3c2x + … + (n–1) ‧
n ‧ cnxn–2 + …
Sostituendo x = 0 si ottiene
2!c2 = f″(0)
Analogamente,
derivando la (3) si trova
3!c3 =
f‴(0)
Ripetendo questo
procedimento si trova la formula generale
![]()
Il risultato è la serie di Taylor:
![]()
▸ (funzioni R ➙ R) La formula di Taylor dimostrata da
Citrini
L’idea base della formula di Taylor è
abbastanza semplice: se la retta tangente è una prima approssimazione di una
data funzione, si può pensare che un’approssimazione migliore si ottenga considerando una
parabola, o un polinomio di grado superiore; e se il coefficiente angolare
della tangente è dato dalla derivata prima, i coefficienti dei termini di grado
più elevato saranno legati alle corrispondenti derivate successiva di f,
supposto che esistono. Siamo dunque indotti a cercare un polinomio (di un
assegnato grado n) che assuma in un punto x0 lo stesso valore e le
stesse derivate (fino all’ordine
n) di f.
La determinazione di tale polinomio è facile: basta notare
che per ogni k ≥ 0 il polinomio
(1) ![]()
si annulla in x0 assieme a tutte le sue derivate
di ordine diverso da k.
Le derivate di ordine inferiore si annullano perché per j
< k si ha:
![]()
Infatti, la derivata prima è:
![]()
la derivata seconda è:
![]()
eccetera, mentre il valore (x – x0) è pari a zero
per x = x0.
Le derivate di ordine superiore si annullano, perché anche
per esse x = x0 rende il numeratore eguale a zero.
Invece la derivata k-esima è pari a:
![]()
e cioè assume identicamente il valore 1.
Dunque la combinazione lineare
![]()
è un polinomio di grado n per il quale risulta
![]()
Possiamo dunque associare associare ad una funzione f dotata
di derivate fino all’ordine n il polinomio di Taylor di grado n:
(2) ![]()
relativo alla funzione f e al punto x0
Si noti che T1(x) coincide con la retta y = f(x0)
+ f′(x0)(x – x0) tangente a y = f(x)
in x0. Invece y = T2(x) si chiama parabola osculatrice a y = f(x) in x0.
Se nella formula (2) poniamo x al posto di x0 e x
+ h al posto di x possiamo scrivere in modo del tutto equivalente:
(3a) ![]()
(3b) ![]()
(3c) ![]()
che mostra il ruolo dei differenziali successivi nella
costruzione del polinomio.
Il cosiddetto resto della formula di Taylor è rappresentato
da:
(4) ![]()
Poiché Tn(x) assume in x0 lo stesso
valore di f(x), come pure ha in x0 il valore delle derivate fino
alla n-esima coincidente con quello di f(x), il resto Rn(x) è una
funzione che si annulla in x0 insieme a tutte le sue derivate fino
all’ordine n, derivate che supporremo senz’altro continue in un intorno di x0.
Inoltre si ha:
![]()
perché si ha:
![]()
e il polinomio Tn(x) ha grado n e quindi la sua
derivata di ordine n + 1 è identicamente nulla (si provi a fare la derivata
terza di x2: la derivata prima è 2x, la derivata seconda è 2 e la
derivata terza è zero).
Supponiamo dapprima che la funzione f sia dotata della
derivata (n+1)-esima nel solo punto x0. Possiamo applicare
ripetutamente la regola di De L’Hôpital al rapporto
![]()
ottenendo, dopo n passaggi, che
![]()
(funzioni r ➙ r) formula di taylor calcolata
mediante una routine vba
▸ (funzioni R ➙ R) Formula di Taylor
calcolata mediante una routine VBA
Per calcolare in modo approssimato il valore del polinomio
di Taylor in un punto x, si può utilizzare la seguente formula:
Public
Function NewFormulaTaylorGrado3(DeltaX As Double,
_
DerivataPrima As Double, _
DerivataSeconda As Double, _
DerivataTerza As Double,_
NumeroIntervalli As Double) As Double
Dim Contatore
As Double
Dim derivata1
As Double
Dim derivata2 As Double
Dim derivata3 As Double
NewFormulaTaylorGrado3 = 0
derivata1 = DerivataPrima
derivata2 = DerivataSeconda
derivata3 = DerivataTerza
For Contatore = 1 To NumeroIntervalli Step 1
derivata2 = derivata2 + derivata3 * (DeltaX /
NumeroIntervalli)
derivata1 = derivata1 + derivata2 * (DeltaX /
NumeroIntervalli)
NewFormulaTaylorGrado3 =
NewFormulaTaylorGrado3 + derivata1 * (DeltaX / NumeroIntervalli)
Next Contatore
End Function
In questa formula ∆x viene suddiviso in intervallini; per ciascuno di essi si
determina il valore esatto della derivata seconda alla fine dell’intervallo a partire dalla derivata
terza costante.
Il valore
approssimato della derivata prima alla fine dell’intervallo è ottenuto supponendo che in tutto l’intervallo la derivata seconda sia
costante ed eguale al suo valore massimo
Il valore approssimato della funzione alla fine
dell’intervallo è ottenuto supponendo che in tutto l’intervallo la derivata
prima sia constante ed eguale al valore massimo approssimato della derivata
prima alla fine dell’intervallo.
Dati i seguenti valori arbitrari:
∆x = 5
f(1) =
6
f(2) =
5
f(3) =
4
(il valore delle
derivate è quello in x0) si ottiene un valore del polinomio di
Taylor = 175,8333645882, molto vicino a quello esatto di 175,8333333333
ottenuto con la formula di Taylor vera e propria:
![]()
(funzioni r ➙ r) teoremi sulla formula di taylor
▸ (funzioni R ➙ R) Proprietà di linearità del
polinomio (operatore) di Taylor
Se c1 e c2 sono costanti, allora
Tn(c1f
+ c2g) = c1Tn(f) + c2Tn(g)
▸ (funzioni R ➙ R) Proprietà di derivazione del
polinomio (operatore) di Taylor: La derivata di un polinomio di Taylor
di f è un polinomio di Taylor di f′
La derivata di un polinomio di Taylor di f è un polinomio di
Taylor di f′; precisamente abbiamo:
(Tnf)′ = Tn-1(f′)
▸ (funzioni R ➙ R) Proprietà di integrazione del
polinomio (operatore) di Taylor: L’integrale indefinito di un polinomio
di f è un polinomio di Taylor di un integrale indefinito di f
Taylor di f è un polinomio di Taylor di
un integrale indefinito di f
L’integrale indefinito di un polinomio di Taylor di f è un
polinomio di Taylor di un integrale indefinito di f. Più precisamente, se è:
![]()
allora abbiamo:
![]()
▸ (funzioni R ➙ R) Proprietà di sostituzione del
polinomio (operatore) di Taylor
Sia g(x) = f(cx)
con c costante. Allora Tn(g(x;a)) = Tn f(cx;ca))
▸ (funzioni R ➙ R) Unicità del polinomio di Taylor
Sia Pn un
polinomio di grado n ≥
1. Siano f,g due funzioni dotate di derivata di ordine n in 0 e supponiamo che
f(x) = Pn(x)
+xng(x)
Allora Pn è il polinomio di Taylor generato da f
in 0.
(funzioni r ➙ r) formula di
mac laurin
▸ (funzioni R ➙ R) Formula di Mac Laurin
La formula di Taylor con punto iniziale x0 = 0
prende il nome di formula di Mac Laurin.
Quando x0
= 0 invece di "sviluppo di Taylor", e "polinomio di Taylor"
si usano spesso i termini "sviluppo di McLaurin", "polinomio di
McLaurin".
La
formula si scrive nel modo seguente:
![]()
dove 0 ≤ θ ≤
1
(funzioni rn ➙ r) Formula di taylor
▸ (funzioni Rn ➙ R) Derivata direzionale iterata di
ordine d di una funzione
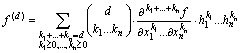
dove è:
![]()
o, equivalentemente
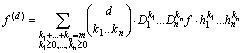
o, equivalentemente
![]()
o, equivalentemente
![]()
▸ (funzioni Rn
➙
R) Esempio di derivata iterata del terzo
ordine di una funzione f : R3 ➙ R
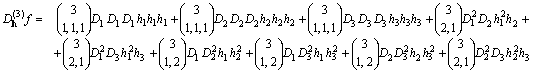
e cioè:
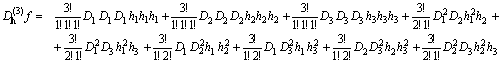
e cioè
![]()
che si può scrivere anche:
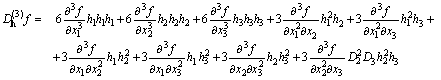
▸ (funzioni Rn
➙
R) Polinomio di Taylor di grado d di una funzione
Scriviamo la formula di Taylor in termini di derivate di
grado successivo e dei loro coefficienti:
![]()
e cioè, esplicitando la formula della derivata iterata:
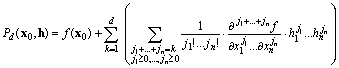
Molti testi, utilizzando un’unica formula di sommatoria
scrivono:
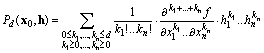
Il coefficiente ![]() si ricava da:
si ricava da:
![]()
in cui il primo fattore è il coefficiente da moltiplicare
alla derivata d-esima nella formula di Taylor, e il secondo fattore è il
coefficiente della derivata d-esima come si ricava dalla formula di f(d)
(funzioni rn ➙ r) resto del polinomio di taylor
▸ (funzioni Rn ➙ R) Formula di Taylor col resto di Peano
Lo sviluppo di Taylor di ordine m per una funzione di
classe Cm nell’intervallo
B(x0,r) di x0 ∈ Rn è dato dalla formula:
[0812121408] 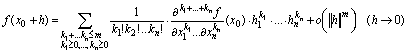
▸ (funzioni Rn ➙ R) Formula di Taylor col resto di Lagrange
Sia f una funzione definita su un aperto U di Rn
ed ivi di classe Ck+1. Fissato in U un punto x0 sia x0
+ h un altro punto di U tale che il segmento x0x sia
interamente in U. Abbiamo allora la formula [0812121550]
If f is a real-valued
function of class Ck + 1 on an open set containing the line segment
L from a to a + h, then there exists a point ξ ∈ L such that:
[0812121550] ![]()
▸ (funzioni Rn ➙
R) resto integrale
Se f è una funzione di classe Ck, con k ≥ 2, su un insieme aperto e convesso
U ∋ 0 di Rn, per ogni x ∈ U è:
[0812290840] 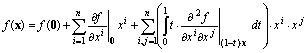
Dimostrazione.
Se n = 1 e 1 ∈ U si ha:
![]()
Se n ≥
1, poniamo ψ(t) = φ(tx) per x ∈
U e 0 ≤ t ≤ 1, e
applichiamo a ψ il calcolo precedente. Tenendo
conto che
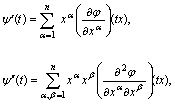
si ottiene la formula del teorema.
▸ (funzioni Rn ➙ R) (resto integrale) Espansione di
Taylor con resto integrale per funzioni C∞
Le funzioni C∞ ammettono una espansione di Taylor
del primo ordine integrale della forma ![]() che può essere scritta nella forma
f = f(x0) + ∑
ci fi.
che può essere scritta nella forma
f = f(x0) + ∑
ci fi.
▸ Formula
di Taylor
Consideriamo un punto x0 del dominio di una
funzione f : Rn ➙ R, e, dato un
altro punto qualsiasi x, denominiamo con v
il vettore x – x0. Definiamo la funzione R ➙ R:
g(s) = f(x0 + s ⋅ v)
con 0 ≤
s ≤
1
Ovviamente si ha:
g(0) = f(x0)
g(1) = f(x0 + v) = f(x)
Dal teorema
fondamentale del calcolo si ha che:
[0702200738] ![]()
La derivata dg/ds si ottiene applicando il chain rule:
[0812311242] ![]()
in modo da ottenere:
[0812311241] ![]()
e cioè, poiché si ha ![]() :
:
[0812311247] ![]()
Pertanto possiamo scrivere la [0702200738] come:
[0702200740] ![]()
e cioè:
[0702200741] ![]()
Se poniamo:
![]()
possiamo scrivere la [0702200741] come:
[0702200742] ![]()
e cioè:
[0702200750] ![]()
▸ Dimostrazione che solo per le funzioni C∞ esiste la espansione di
(Dimostrazione che ![]() è una funzione C∞ )
è una funzione C∞ )
Anzitutto, dimostriamo che se g è C∞, anche g(sp) è C∞. Infatti la composizione di
funzioni continue è continua; g è una funzione continua, e s ⋅ p è continua se le sue funzioni
componenti s ⋅ p1, s ⋅ p2, …, s ⋅ pn sono continue. Le funzioni componenti sono
continue perché sono lineari:
s ⋅ (k1p + k2q)
= k1 ⋅ s ⋅ p + k2 ⋅ s ⋅
q
Applichiamo il seguente
teorema: If h(p,s) is a C1 function of (p,s) ∈ Rd+1 and k(p) = ![]() , then k is C1 and
, then k is C1 and ![]()
Da tale teorema ricaviamo subito che ![]() esiste, perché
esiste, perché ![]() è di
classe C1.
è di
classe C1.
Poiché per il teorema è:
![]()
possiamo porre:
![]()
![]()
e concludere che ![]() esiste, perché
esiste, perché ![]() è C1.
è C1.
Reiterando il procedimento possiamo porre:
![]()
![]()
e concludere che ![]() esiste, perché
esiste, perché ![]() è C1.
è C1.
Il procedimento può essere reiterato un numero infinito di
volte, e mostra quindi che ![]() è C∞.
è C∞.
Come si vede, un ruolo cruciale viene giocato nella
dimostrazione dal fatto che g ∈
C∞. Se g ∈ C∞ l’espansione di Taylor:
![]()
scritta anche come:
![]()
avrà le gi di classe C∞.
Poiché si può
dimostrare che è ![]() , resta
dimostrato che qualsiasi tangente nel punto m è combinazione lineare dei coordinate vector fields.
, resta
dimostrato che qualsiasi tangente nel punto m è combinazione lineare dei coordinate vector fields.
▸ (funzioni Rn ➙ R) (resto integrale): Se la funzione è
Ck il resto integrale della espansione di Taylor con integrali delle
derivate di ordine n è Ck-n
(funzioni r ➙ rn) formula di taylor
▸ (funzioni R ➙ Rn)
Formula di Taylor
La formula è:
[0506281045] ![]()
dove Rm(t,t0) ha la proprietà:
[0506281046] ![]()
(funzioni rn ➙ rm) formula di taylor
▸ Il calcolo multivariato delle
funzioni a valori vettoriali si basa sull’importante risultato che il limite di
una funzione Rn ➙ Rm è dato dai limiti delle
funzioni componenti
Il limite di una funzione Rn
➙ Rm è dato dai limiti delle funzioni componenti
Sia F = (f1,…,fm) una funzione A ⊂ Rn ➙ Rm, e sia p un punto di
accumulazione per A. Allora: limx➙p f(x) = ℓ = (ℓ1, …, ℓm) sse per ogni i = 1, …, m si ha limx➙pfi(x) = ℓi
▸ (funzioni Rn
➙ Rm)
Derivata direzionale iterata di ordine
d
La derivata direzionale iterata di ordine r di una funzione
F : Rn ➙
Rm è un vettore di Rm ciascun componente del quale è la
derivata direzionale iterata di ordine k di una delle funzioni componenti:
Dv(d)F
= (Dv(d)f1,
…., Dv(d)fm)
▸ (funzioni Rn ➙ Rm) Polinomio di Taylor di ordine k
Il polinomio di Taylor di grado d relativo ad una funzione a
valori vettoriali è formato dai polinomi di grado d P1d,
…, Pmd delle singole funzioni componenti:
Pd(x0,h) = ( P1d(x0,h), …, Pmd(x0,h) )
(funzioni di variabile complessa)
formula di taylor
▸ Consideriamo,
nel campo complesso, una serie di potenze
[0812311856] a0
+ a1z + a2z2 + …
dove i
coefficienti a0, a1, … sono numeri complessi al pari della variabile indipendente
z
▸ Sappiamo
che se una serie di potenze converge per qualche valore di z non nullo e non
converge per qualsiasi valore di z, esiste un numero positivo r tale che la
serie data è convergente assolutamente in ogni punto interno al cerchio di
raggio r e centro l’origine mentre non converge per
alcun valore di z in modulo maggiore di r.
Tale cerchio
chiamasi cerchio di convergenza della serie data, ed r chiamasi raggio di
convergenza
Se una serie di
potenze converge soltanto per z = 0, dicesi che il suo raggio di convergenza è
nullo; se la serie converge per qualsiasi valore di z, dicesi che il suo raggio
di convergenza è infinito.
Se il raggio di
convergenza r della serie [0812311856] è diverso da zero, la serie
converge totalmente (e quindi anche uniformemente) in ogni cerchio avente il
centro nell’origine e raggio minore di r.
▸ Nei
punti interni al cerchio di convergenza della [0812311856] la somma della serie è una
funzione continua
▸ Consideriamo
la serie derivata dalla [0812311856]:
[0812311857] a1
+ 2a2z + 3a3z2 + …
Ragionamenti
analoghi a quelli adoperati nel caso reale permettono di dimostrare che la
serie [0812311856] e la sua serie derivata hanno lo stesso cerchio di
convergenza
▸ Se
la serie di potenze:
![]()
ha per raggio di
convergenza r > 0, per ogni z in modulo minore di r, la f(z) è derivabile, e
si ha:
![]()
▸ Se
il raggio di convergenza della serie:
[0812311859] ![]()
è diverso da
zero, la somma f(z) di tale serie è una funzione indefinitamente derivabile in
ogni punto interno al proprio cerchio di convergenza; e le derivate di f(z)
possono essere calcolate a partire dalla [0812311859] mediante successive derivazioni termine
a termine:
[0812311900] ![]()
Ora, se nella [0812311859] e nella [0812311900] poniamo z = 0 otteniamo:
![]()
![]()
da cui risulta:
[0812311901] ![]()
in tutti i punti
interni al cerchio di convergenza della serie.
Se una funzione
f(z) della variabile complessa z è indefinitamente derivabile nell’origine, la serie di potenze [0812311901] si chiama serie di Mac Laurin.
▸ Le
nozioni di raggio e cerchio di convergenza si pongono subito anche per le serie
di potenze
[0812311902] ![]()
essendo z0
un numero complesso
Evidentemente le
cose dette si trasportano immediatamente anche a queste serie.
In particolare,
se il cerchio di convergenza della serie [0812311902] non si riduce al punto z0
e se f(z) è la somma della serie, allora f(z) è continua e indefinitamente
derivabile nell’interno del cerchio di convergenza;
le sue derivate si possono ottenere mediante successive derivazioni per serie,
e risulta altresì:
a0 =
f(z0)
![]()
e quindi la [0812311902] diventa:
[0812311903] ![]()
Se una funzione
f(z) della variabile complessa z è indefinitamente derivabile nel punto z0
la serie [0812311903] è la serie di Taylor della f(z) relativa al punto iniziale
z0
Riassumendo, se
il cerchio di convergenza della serie [0812311902] non si riduce al solo punto z0,
la [0812311903]
è la serie di Taylor della propria somma.
Infine, se
ricordiamo che nel campo complesso si è posto per definizione:
[0812311904] ![]()
[0812311905] ![]()
[0812311906] ![]()
convergendo le
serie, a secondo membro, in tutto il piano complesso, possiamo, in virtù di
quanto abbiamo visto, dire che le funzioni ez, sin z, cos z, sono
derivabili, e derivando termine a termine tali serie si ottiene:
D[ex] = ex
D[sin z] = cos z
D[cos z] = – sin z
come nel campo
reale.
▸ Consideriamo
serie
[0812311907] ![]()
essendo z0
un numero complesso.
Evidentemente le
cose dette per la serie di Mac Laurin si trasportano immediatamente anche a
queste serie.
In particolare,
se il cerchio di convergenza della serie [0812311907] non si riduce al punto z0
e se f(z) è la somma della serie, allora f(z) è continua e indefinitamente
derivabile nell’interno del cerchio di convergenza;
le sue derivate si possono ottenere mediante successive derivazioni per serie,
e risulta altresì:
a0 =
f(0)
![]()
in modo che la [0812311907] diventa:
[0812311908] ![]()
Se una funzione
f(z) della variabile complessa z è indefinitamente derivabile nel punto z0,
la serie [0812311908] è la serie di Taylor della f(z) relativa al punto iniziale
z0.
Sicché se il
cerchio di convergenza della serie [0812311907] non si riduce al solo punto z0,
la [0812311907]
è la serie di Taylor della propria somma.